dU = TdS - pdV dF = - SdT - pdV
dH = TdS + Vdp dG = - SdT + Vdp
Условия равновесия и критерий направления
химических реакций
Условия равновесия можно сформулировать следующим образом:
Ø в состоянии равновесия системы её термодинамические потенциалы имеют минимальное значение при постоянстве своих независимых переменных, а энтропия имеет максимальное значение при постоянстве U - внутренней энергии, H - энтальпии, V - объема или p - давления.
В аналитическом виде эти условия выглядят так:
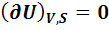
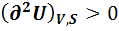 min
min
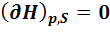
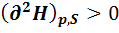
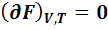
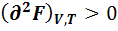
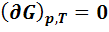
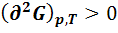
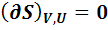
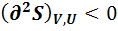 max
max
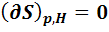
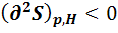
 То есть в состоянии равновесия первая производная (нарастание или уменьшение функции) равна нулю. Это означает, что это точка экстремума. А какой это экстремум (min или max) первая производная сказать не может. Это характеризует вторая производная. Если вторая производная > 0, то значит это min экстремум. Все функции, кроме энтропии, принимают min значение в состоянии равновесия.
То есть в состоянии равновесия первая производная (нарастание или уменьшение функции) равна нулю. Это означает, что это точка экстремума. А какой это экстремум (min или max) первая производная сказать не может. Это характеризует вторая производная. Если вторая производная > 0, то значит это min экстремум. Все функции, кроме энтропии, принимают min значение в состоянии равновесия.
Любая реакция может протекать самопроизвольно только в направлении, приближающем систему к состоянию равновесия.
Другим условием принципиальной осуществимости процесса, т.е. возможности протекания реакции в прямом направлении без затраты работы является неравенство: 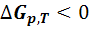

 Чем больше химическое
Чем больше химическое
|
|
|
 сродство реагентов, т.е.
сродство реагентов, т.е.
|
|
купность данных веществ
от состояния равновесия
|
|
|
 процессов), тем сильнее
процессов), тем сильнее стремление к протеканию
процесса, тем больше
убыль изобарного потенциала.
И наоборот, условием принципиальной невозможности процесса является неравенство: 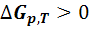
Следует подчеркнуть, что этот прогноз совершенно не зависит от механизма реакции, от химического пути, по которому протекает процесс, поскольку величина DG равна разности значений энергий Гиббса продуктов реакции и исходных реагентов. Следовательно, DG не дает информации о самом процессе и, в частности, о его скорости.
Между принципиальной осуществимостью процесса и его практической реализацией дистанция огромного размера. Вопреки условию DG < 0 реакцию провести не всегда удается.
Нам известно, что
DF = DU - TDS - изохорно-изотермический потенциал
DG = DH - TDS - изобарно-изотермический потенциал
Следовательно, в самопроизвольно протекающих процессах:
DF = DU - TDS < 0
DG = DH - TDS < 0
Отсюда, вытекают важные следствия:
Если DH > 0 и DS > 0, то |DH| < |TDS| процесс самопроизвольно
протекает при высоких температурах
Если DH < 0 и DS < 0, то |DH| > |TDS| процесс самопроизвольно
протекает при низких температурах
Если DH < 0 и DS > 0, то DG < 0 процесс возможет без ограничений
при любых температурах
Если DH > 0 и DS < 0, то DG > 0 процесс невозможен
Для многих не слишком сложных реакций первый (энтальпийный) фактор отражает обычное повышение устойчивости системы при уменьшении запаса её внутренней энергии, которое проявляется в тенденции к большей агрегации вещества, укрупнению частиц.
Второй же фактор (энтропийный) отражает тенденцию к дезагрегации, к усилению процессов диссоциации на более простые частицы, происходящие под действием теплового движения частиц.
В реакциях, приближающих систему к состоянию равновесия, эти два фактора действуют в противоположных направлениях, и общее течение процесса определяется действием преобладающего фактора и сопровождается сближением величин DН и ТDS до их равенства в состоянии равновесия: DНРАВН = ТDSРАВН.
Так как тепловой эффект реакции обычно мало зависит от концентрации реагирующих веществ, то достижение равновесия практически полностью определяется концентрационной зависимостью изменения энтропии.
Стандартные состояния веществ, основные стандартные состояния элементов
При изучении термодинамических свойств веществ и параметров реакций большое значение приобрело понятие стандартное состояние.
Для индивидуальных твердых веществ и жидкостей в качестве стандартного принимают их состоянии при р = 1 атм. и данной температуре.
Для индивидуальных газов - это - состояние в виде гипотетического идеального газа, фугитивность (летучесть) которого равна единице при данной температуре, а энтальпия вещества в этом состоянии равна энтальпии реального газа при той же температуре и при р = 0.
Справочные значения термодинамических функций различных веществ обычно относятся к их стандартному состоянию, а параметра реакций к условиям, когда каждое из веществ находится в стандартном состоянии.
Стандартные значения отмечают верхним индексом °: 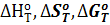
Как правило, основным стандартным состоянием элемента считается его наиболее термодинамически устойчивая форма для данной температуры и р = 1 атм. Например:
для углерода - графит,
для ртути - жидкость,
для кислорода - газ, с двухатомными молекулами О2.
Обычно выбирают стандартную температуру равную 25°С или 298,15 К.
Свойство аддитивности термодинамических потенциалов
Термодинамические потенциалы 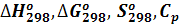 обладают свойствами аддитивности, операции с ними сводятся к простому алгебраическому суммированию:
обладают свойствами аддитивности, операции с ними сводятся к простому алгебраическому суммированию:
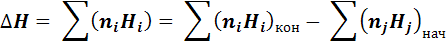
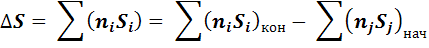
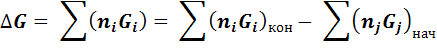
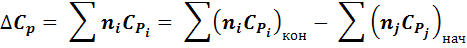
Расчет изменения изобарно-изотермического
потенциала реакций
Изобарно-изотермический потенциал вещества или реакции можно вычислить из значения теплоты образования, энтропии и теплоемкости с учетом третьего закона термодинамики по уравнению:
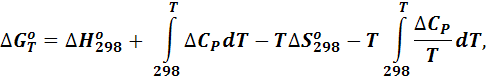
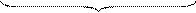 |
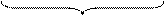
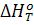
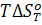
которое является развернутой формой уравнения:
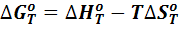
Пусть зависимость теплоемкости от температуры выражается функцией:
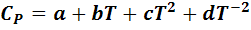 (1)
(1)
Для реакции типа А + В = С + D имеем:
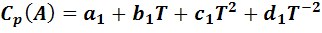
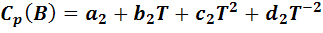
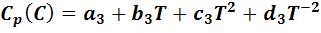
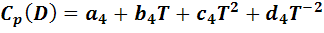
Из этих уравнений вычислим температурную зависимость изменения теплоемкости как разность теплоемкостей продуктов реакции и реагентов:
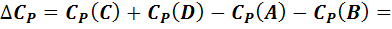
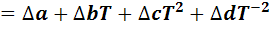 (2)
(2)
При этом Da = a3 + a4 - a1 -a2
Db = b3 + b4 - b1 - b2
Dc = c3 + c4 - c1 - c2
Dd = d3 + d4 - d1 - d2
Тепловой эффект реакции 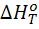 определяется из теплоемкости простым интегрированием уравнения (2) в определенном интервале температур. Если в качестве стандартной температуры принять 298,15°К, то уравнение для теплового эффекта реакции имеет вид:
определяется из теплоемкости простым интегрированием уравнения (2) в определенном интервале температур. Если в качестве стандартной температуры принять 298,15°К, то уравнение для теплового эффекта реакции имеет вид:
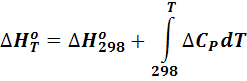
Подставим уравнение для теплоемкости (2):
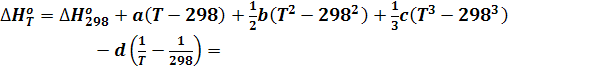
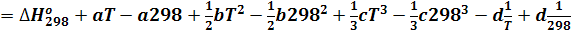
Включим постоянные величины в член А, т.е.
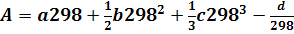
Получим конечное выражение для теплового эффекта реакции:
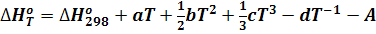 (3)
(3)
Это уравнение можно использовать лишь в интервале температур, где нет фазовых превращений.
С учетом фазовых и полиморфных превращений для расчета теплового эффекта используется уравнение, представляющее собой сумму членов для каждой фазы данного вещества в рассматриваемом интервале температур плюс член, представляющий сумму значений теплоты полиморфных и фазовых превращений:
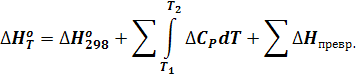
Изменение энтропии для реакции при 298°К можно вычислить по уравнению:
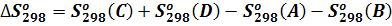
Изменение энтропии реакции при других температурах вычисляется по уравнению:
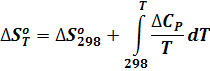
Учитывая уравнение для теплоемкости (2) получим:
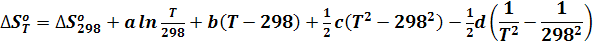
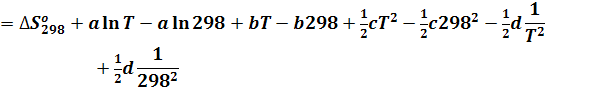
Включим постоянные величины в член В, т.е.
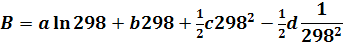
Получим конечное выражение для изменения энтропии:
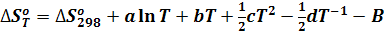 (4)
(4)
Постоянные А в уравнении (3) и В в уравнении (4) не зависят от температуры, а зависят от коэффициентов a, b, c и d.
Подставляя функции изменения энтальпии и энтропии, т.е. уравнения (3) и (4) в выражение 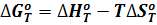 получим полное, точное уравнение для расчета термодинамического потенциала:
получим полное, точное уравнение для расчета термодинамического потенциала:
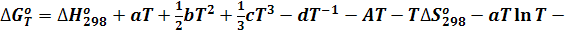
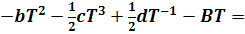
приведем подобные
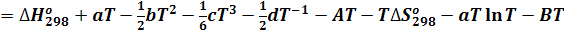
Объединим члены
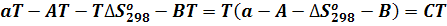
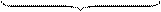 |
C
Получим:
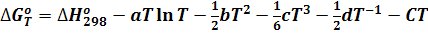 (5)
(5)
Напоминаю, что это полное точное уравнение для расчета изобарно-изотермического потенциала реакции.
В некоторых справочниках даются другие формы этого уравнения:
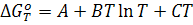
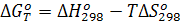
Это приближенные уравнения и методы расчета.
К приближенным методам расчета приходится обращаться, прежде всего, из-за недостатка необходимых экспериментальных данных для точного расчета. Кроме того, экспериментальные данные часто имеют такие погрешности, что уравнения типа (5) могут быть заменены приближенными двух- и трехчленными уравнениями без ущерба для точности. И наконец, приближенные методы широко применяют для ориентировочных подсчетов для оценки возможности протекания реакции в требуемом направлении.
Преимуществом приближенных методов расчета термодинамических потенциалов является меньшая трудоемкость и большая доступность в практической работе.
Еще один метод расчета изобарно-изотермического потенциала реакции, также являющийся точным методом - это
Метод Тёмкина-Шварцмана
Исходное уравнение для изменения свободной энергии Гиббса, которое использовали авторы, записывается в виде:
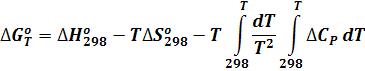 (6)
(6)
Оставляя обоснование формы этого уравнения на самостоятельную проработку, замечу только, что из сравнения с развернутой формой уравнения Гиббса-Гельмгольца следует, что:
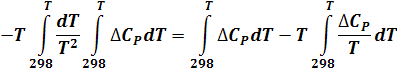 (7)
(7)
Если изменение теплоемкости задается уравнением (1), то при подстановке уравнения (1) в уравнение (6) получим:
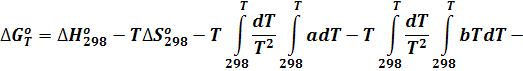
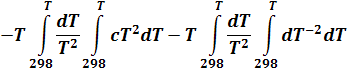
Разделим все члены этого уравнения на Т и вынесем постоянные a, b, c, d из знака интеграла:
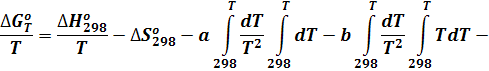 (8)
(8)
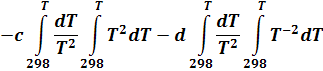
Значения подынтегральных функций этого уравнения приведены в литературе. Авторы (Темкин и Шварцман) обозначили эти функции через Мо, М1, М2, М-2.
В этом случае уравнение (8) приобретает следующий вид:
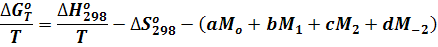 (9)
(9)
Значения функций Мо, М1, М2, М-2 при отсутствии табличных данных можно вычислить по уравнениям:
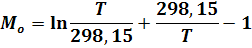
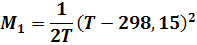
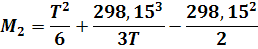
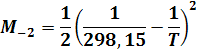
Если некоторые члены уравнения (9) отсутствуют (например, с или d), расчет упрощается.
Приведенный потенциал, новые термодинамические функции
Рассмотрим ещё один вид термодинамических функций и их изменение в результате реакций.
Разделим основное уравнение G = H - TS на температуру:
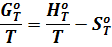
и вычтем из правой и левой частей отношение 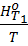 :
:
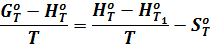 (10)
(10)
где Т1 - температура, принимаемая в качестве базисной.
Использование функций 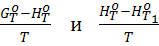 имеет некоторые преимущества при рассмотрении влияния температуры на химическое равновесие.
имеет некоторые преимущества при рассмотрении влияния температуры на химическое равновесие.
Изменение правой из них 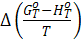 сравнительно слабо зависит от температуры, что позволяет легче осуществлять интерполяцию и экстраполяцию по температуре. Кроме того, значения этой функции для веществ, сходных по составу и строению, близки между собой, что позволяет оценивать недостающие величины.
сравнительно слабо зависит от температуры, что позволяет легче осуществлять интерполяцию и экстраполяцию по температуре. Кроме того, значения этой функции для веществ, сходных по составу и строению, близки между собой, что позволяет оценивать недостающие величины.
Иногда эти функции делят на газовую постоянную R.
Функции 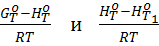 и соответственно
и соответственно 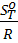 являются безразмерными, т.е. их значения не зависят от единиц измерения и количества вещества, что имеет свои преимущества. Они характеризуют определенное свойство данного вещества.
являются безразмерными, т.е. их значения не зависят от единиц измерения и количества вещества, что имеет свои преимущества. Они характеризуют определенное свойство данного вещества.
В качестве базисной температуры Т1 принимают 0°С или 298,15°К. Переход от одного температурного базиса к другому осуществляется по уравнениям:
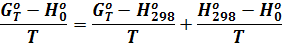 (11)
(11)
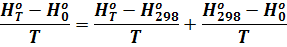
Существенно то, что методы статистической термодинамики дают возможность непосредственно определять значения функции 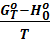
Использование в качестве базисной температуры 298,15°К удобно в тех случаях, когда имеются данные для высокотемпературных составляющих энтальпии 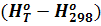 и энтропии
и энтропии 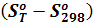 . С их помощью функция
. С их помощью функция 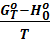 определяется по уравнению:
определяется по уравнению:
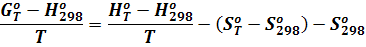 (12)
(12)
которое легко получается из уравнения (10). При этом для температуры 298,15°С, как следует из уравнения (10) 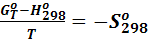
Названия этих функций ещё не унифицированы.
Величина 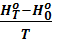 называется большей частью функцией энтальпии.
называется большей частью функцией энтальпии.
Для величины 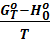 применяют термины: «функция свободной энергии», функция изобарного потенциала», «функция свободной энтальпии» и «функция энергии Гиббса».
применяют термины: «функция свободной энергии», функция изобарного потенциала», «функция свободной энтальпии» и «функция энергии Гиббса».
При базисной температуре 0°К вместо этой функции часто пользуются величиной 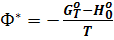
Ф* называется приведенным термодинамическим потенциалом или Ф*-потенциалом.
Изменения этих функций в результате реакции связаны между собой уравнением:
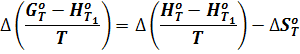
При базисной температуре Т1 = 298,15°К и температуре Т = 298,15°К имеет место равенство, аналогичное уравнению (11):
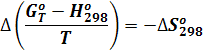
Определить значение 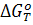 или константы равновесия можно по формулам:
или константы равновесия можно по формулам:
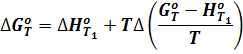
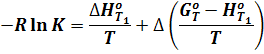
Эти формулы можно использовать в практических расчетах благодаря наличию готовых табличных значений 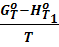 для большого числа веществ в значительном интервале температур.
для большого числа веществ в значительном интервале температур.
 2014-01-25
2014-01-25 1085
1085








