Равномерное движение
При равномерном движении точки по траектории любой формы модуль скорости v=const, следовательно постоянна и алгебраическая скорость v t, которая может отличаться от v только знаком.
Так как 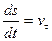 , то
, то 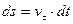 . Если принять при
. Если принять при 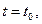
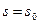 , то после интегрирования получим
, то после интегрирования получим
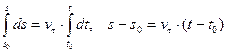 или
или 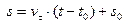
Можно также записать 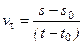
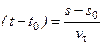
Равнопеременное движение
Равнопеременным движением называется такое движение точки по траектории любой формы, при котором касательное ускорение постоянно, т.е. a t = const Движение называется равноускоренным если алгебраическая скорость v t и касательное ускорение a t имеют одинаковые знаки. Если v t и a t имеют разные знаки, то назыется равнозамедленным. Получим формулы для алгебраической скорости и расстояния при равнопеременном движении.
Имеем:
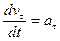 ,
, 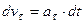 .
.
Если принять при 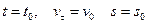 , то после интегрирования получим
, то после интегрирования получим
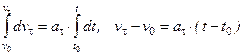 или
или 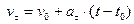 .
.
Можно также записать 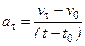
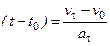
Далее 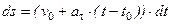 и после интегрирования
и после интегрирования
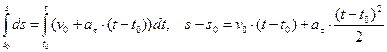
или 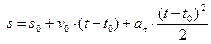 .
.
Можно также записать 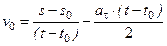
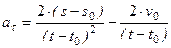
Если решить квадратное уравнение, то можно найти 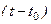 .
.
 2014-01-25
2014-01-25 714
714







