Разложим ускорение и скорость точки на составляющие, параллельные осям декартовой системы координат. Получим
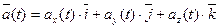
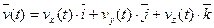 (2-5)
(2-5)
После дифференцирования
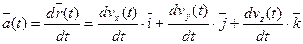 (2-6)
(2-6)
Отсуда следует
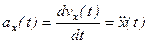
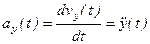
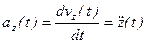 (2-7)
(2-7)
Проекция ускорения точки на какую-либо координатную ось равна второй производной по времени от соответствующей координаты этой точки.
Модуль ускорения и направляющие косинусы равны:
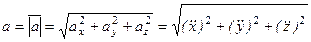 (2-8)
(2-8)
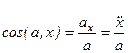
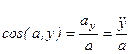
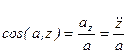 (2-9)
(2-9)
Если точка движется в плоскости, то, выбрав оси координат Ox и Oy в этой плоскости, получим:
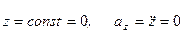
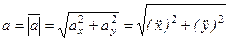
Для прямолинейного движения точки координатную ось, например ось Ox, направляем по траектории. Тогда
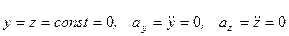
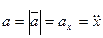
Ускорение точки при естественном способе задания движения.
Скорость точки равна 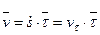 .
.
В соответствии с определением ускорения
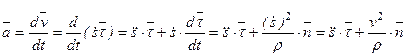 .
.
Или 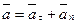 (2-10)
(2-10)
Таким образом получено разложение вектора ускорения точки по осям естественного трехгранника.
Часть ускорения 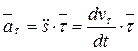 (2-11)
(2-11)
называется касательной составляющей ускорения.
Другая часть ускорения 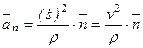 (2-12)
(2-12)
называется нормальной составляющей ускорения. Она направлена внутрь вогнутости траектории, т.е. в сторону положительного направления единичного вектора главной нормали 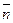 .
.
Формулы для проекции ускорения на естественные оси:
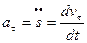
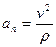
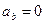
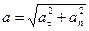
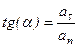
Касательная составляющая 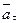 , при
, при 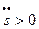 направлена по направлению вектора
направлена по направлению вектора 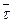 , при
, при 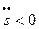 противоположно
противоположно 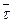 .
.
 2014-01-25
2014-01-25 928
928








