Координаты центров тяжести однородных тел

Для однородного тела вес 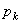любой его части пропорционален объему 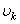этой части: 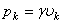, а вес Р всего тела пропорционален объему V этого тела 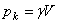, где 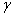- вес единицы объема.

Подставив эти значения Р и 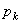в предыдущие формулы, мы заметим, что в числителе 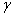как общий множитель выносится за скобку и со­кращается с 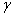в знаменателе. В результате получим:

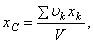
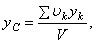
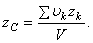
Как видно, центр тяжести однородного тела зависит только от его геометрической формы, а от величины 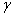не зависит. По этой причине точку С, координаты которой определяются формулами, называют центром тяжести объема V.

Путем аналогичных рассуждений легко найти, что если тело пред­ставляет собой однородную плоскую и тонкую пластину, то для нее

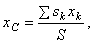
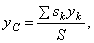
где S - площадь всей пластины, a 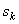- площади ее частей.

Точку, координаты которой определяются формулами называют центром тяжести площади S.

Точно так же получаются формулы для координат центра тя­жести линии:

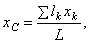
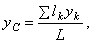
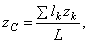
где L — длина всей линии, l — длины ее частей.

Таким образом, центр тяжести однородного тела определяется, как центр тяжести соответствующего объема, площади или линии.