При рассмотрении пространственной системы сил, приложенных к твердому телу, применяется понятие векторного момента силы относительно точки.
Векторным моментом силы относительно точки называют вектор, приложенный в этой точке и равный по модулю произведению силы на плечо силы относительно этой точки. Векторный момент силы направлен перпендикулярно плоскости, в которой лежат сила и моментная точка, таким образом, что с его конца можно видеть стремление силы вращать тело против движения часовой стрелки.
Условимся векторный момент силы 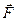 относительно точки О обозначать
относительно точки О обозначать 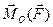 , а его числовую величину –
, а его числовую величину – 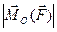 . Тогда, согласно определению,
. Тогда, согласно определению,
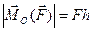 .
.
Как и для алгебраического момента,
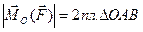 .
.
Справедлива формула
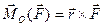 ,
,
где r – радиус-вектор, проведенный из моментной точки О в точку приложения сил или любую другую точку линии действия силы.
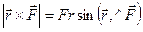 ,
,
Вектор 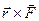 перпендикулярен плоскости треугольника OAB.
перпендикулярен плоскости треугольника OAB.
Если сила 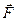 дана своими проекциями
дана своими проекциями 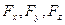 на оси координат и даны координаты x, у, z точки приложения этой силы, то векторный момент относительно начала координат, вычисляем по формуле
на оси координат и даны координаты x, у, z точки приложения этой силы, то векторный момент относительно начала координат, вычисляем по формуле
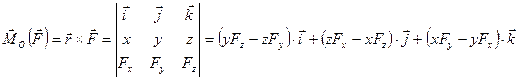 ,
,
где 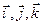 – единичные векторы, направленные по осям координат.
– единичные векторы, направленные по осям координат.
Используя вышеприведенную формулу, можно выделить проекции 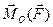 на оси координат:
на оси координат:
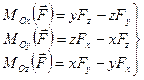
Модуль векторного момента 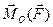 и косинусы углов с осями координат определяем по формулам
и косинусы углов с осями координат определяем по формулам
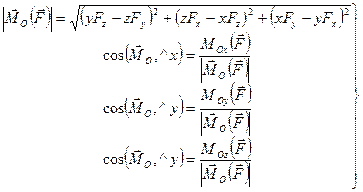
 2014-01-25
2014-01-25 909
909








