2014-01-25
968
Две пары сил называют эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.
Пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющей одинаковый с первой парой алгебраический момент.
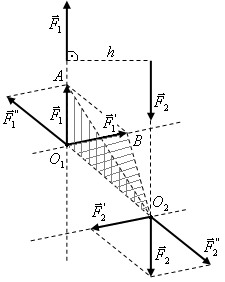
Пусть на твердое тело действует пара сил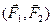 
с алгебраическим моментом М (рис. 11). Перенесем силу 
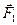в точку 
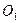, а силу 
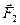– в точку 
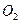проведем через точк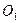и и 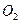две любые параллельные прямые, пересекающие линии действия сил пары и лежащие, следовательно, в плоскостидействия заданной парьы сил. Соединив прямой точк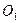и и 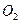, разложим силы 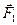в точке 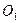и 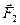в точке 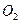по правилу шipаллелограмма, как указано на рис. 11. Тогда
; 
.
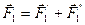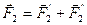Так как силы 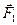и 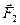образуют пару сил, то
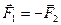
и, следовательно,
; 
.
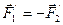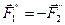Итак,
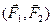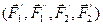P 
P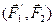 
,
так как
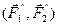P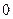 
;
следовательно, эту систему двух сил можно отбросить.
Таким образом, заданную пару сил 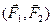заменим другой парой сил 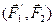. Докажем, что алгебраические моменты у этих пар сил одинаковы. Направление вращения у них одно и то же. Имеем
;
.
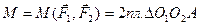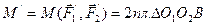Но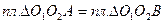 
, так как эти треугольники имеют общее основание 
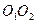и равные высоты (их вершины расположены на общей прямой, параллельной основанию).
Выводы:
а) пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия;
б) у пары сил можно изменять плечо и силы, сохраняя при этом алгебраический момент пары и плоскость действия.
