Признак эквивалентности двух пар сил

Теорема. Для эквивалентности двух пар сил необходимо и достаточно, чтобы моменты этих пар были геометрически равны.

Доказательство.

Необходимость.

Дано: две пары сил 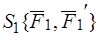и 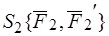эквивалентны.

Следует доказать, что моменты этих пар геометрически равны:

.

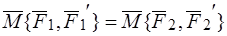Доказательство: Воспользуемся общим признаком эквивалентности двух систем сил 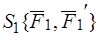и 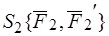, согласно которому следует, что

, .

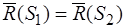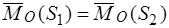Но главный вектор любой пары равен нулю, главный момент пары равен моменту пары:

, .

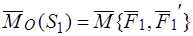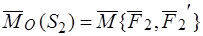Следовательно:

.

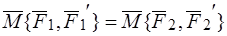Достаточность.

Даны две пары сил 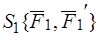и 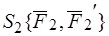, причем моменты этих пар геометрически равны, то есть .

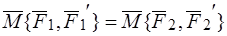Доказать, что пары эквивалентны: ~.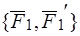

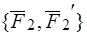Доказательство:

Главные векторы пар равны нулю и следовательно равны между собой 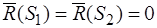. Моменты пар равны главным моментам пар и, по условию, равны между собой:

.

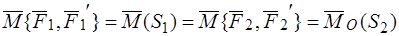Тогда, согласно общему признаку эквивалентности двух систем сил, пары эквивалентны.