2014-01-25
1023
Теорема. Для того, чтобы две системы сил были эквивалентны, необходимо и достаточно, чтобы у этих систем были геометрически равны соответственно главные векторы и главные моменты относительно одного и того же полюса.
Доказательство.
Необходимость.
Дано: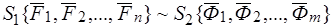 
.
Следует доказать, что у этих систем сил равны главные векторы и главные моменты относительно одного и того же полюса, то есть что
, 
.
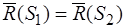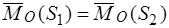Доказательство: Системы сил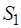 
и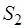 
эквивалентны, следовательно, одна из другой могут быть получены с помощью элементарных операций. Но элементарные операции не изменяют главный вектор и главный момент системы сил – второе (геометрическое) свойство элементарных операций, поэтому , .
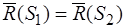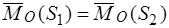Достаточность.
Дано: две системы сил 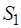и 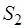, главные векторы и главные моменты которых равны, то есть , .
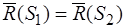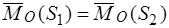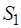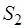Доказать, что системы и эквивалентны.
 |
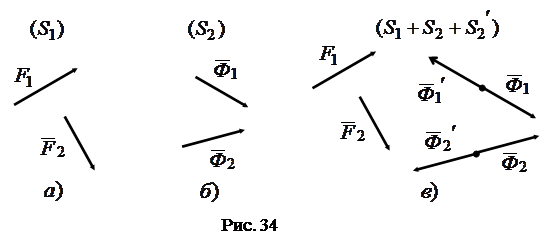Доказательство: Не ограничиваясь в общности, проводим доказательство в предположении, что каждая из систем
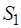и 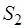состоит из двух сил, то есть пусть даны системы сил 
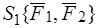и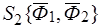 
(рис 34а). В силу основной леммы статики системы сил 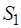и 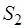, содержащие произвольное число сил всегда при помощи элементарных операций могут быть приведены к двум силам, при этом главные векторы и главные моменты этих систем сил не изменяются. Рассмотрим дополнительную систему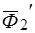 
, силы которой пряморотивоположны силам системы :
, 
.
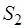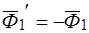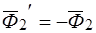Тогда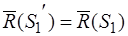 
, 
.
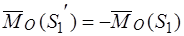Системы сил 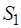(рис. 34а) и 
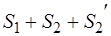(рис. 34в) эквивалентны:
,
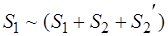так как система 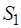может быть получена из системы 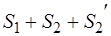отбрасыванием прямопротивоположных сил 
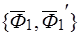и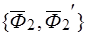 
.
Рассмотрим систему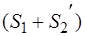 
, состоящую из сил 
.
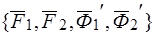Главный вектор: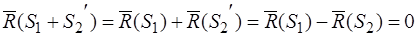 
.
Главный момент:
.
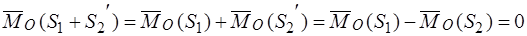Согласно основной лемме статики систему сил 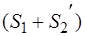можно заменить двумя силами 
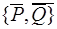. Тогда ~
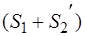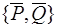. У эквивалентных систем сил равны главные моменты и главные вектор: поэтому
,
,
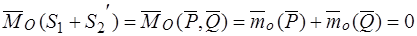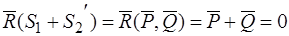то есть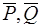 
– прямопротивоположные силы, которые можно отбросить. Таким образом:
,
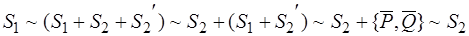или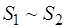 
.
Теорема доказана.
