Лекция Теплофизические свойства горных пород

Теплофизические свойства горных пород: теплопроводность, l 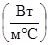; теплоемкость, c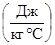; температуропроводность, а (м²/c); теплоусвояемость b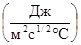, определяющие процессы распространения теплоты, зависят от их химического состава, кристаллической системы составляющих минералов, их размеров, содержания кристаллической и стекловидной (аморфной) фаз, пористости, степени насыщения влагой, температуры, давления и т.д.). Коэффициент теплопроводности численно равен количеству теплоты, проходящему в единицу времени через две противоположные грани единицы объема породы, на которых поддерживается разность температур в один градус. Таким образом, теплопроводность горных пород характеризует их степень проводимости теплоты. Механизм теплопроводности монолитных горных пород с позиции квантовой теории объясняется переносом энергии электронами и фононами (звуковыми квантами) в потенциальном поле, создаваемом кристаллической решеткой. Фононы возникают в результате наложения колебаний узлов кристаллической решетки твердого тела. При движении по кристаллической решетке фононы, сталкиваясь друг с другом или с дефектами кристаллической решетки, разрушаются. При этом образуются новые фононы. Фонон, обладая некоторой длиной свободного пробега l _ф, переносит энергию на эту длину. Так как количество дефектов в реальных кристаллах очень велико, то время существования каждого фонона незначительно. Это, в свою очередь, сказывается на величине теплопроводности.

Теплопроводность реальных кристаллов и пород, которая по сравнению, например, с металлами, сравнительно невелика. Вместе с тем, при увеличении чистоты кристаллов их теплопроводность значительно возрастает. В связи с тем, что породы в абсолютном большинстве являются диэлектриками и полупроводниками, и количество свободных электронов в них мало, теплопроводность их в основном обусловлена фононной (решеточной) составляющей теплопроводности (при температуре 300К электронная составляющая теплопроводности l_эл £ 10^-8 Вт/(м°С).

Зависимость коэффициента теплопроводности монолитных твердых тел от длины пробега фононов l _ф, а также скорости распространения упругих волн v_у, плотности пород r_п и их изохорной удельной теплоемкости с_v предложенная Д.Займаном, имеет вид

l = 1/3 v_у l _фr_пс_v (2.1)

Если рассматривать горную породу как "твердый раствор", образованный совокупностью различных материалов, то, зная теплопроводность каждого из минералов, можно вычислить и теплопроводность самой породы.

Для расчета теплопроводности отдельных минералов l_i при этом рекомендуется использовать формулу, предложенную А.Миснаром:

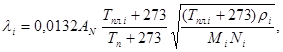(2.2)

где Т_п, Т_пл.i – соответственно температура пород, при которой осуществляется определение l_i, и температура плавления минерала, °С; r_i – плотность минерала кг/м³; М_i – атомный вес минерала; N_i – число атомов в химической формуле; А_N – коэффициент, зависящий от сингонии кристалла и определяемый опытным путем (А_N соответственно равен 1,12 при кубической сингонии, 2,58 – при триклинной, 1,99 – при моноклинной, 2,55 – при гексагональной).

При известных значениях теплопроводностей минералов, слагающих горную породу, для определения теплопроводности породы используется следующая последовательность:

1. Все минералы группируются попарно, образуя т.н. биминеральные смеси.

2. Рассчитываются теплопроводности биминеральных смесей.

3. По найденным теплопроводностям биминеральных смесей составляются новые "условные" биминеральные смеси и вновь рассчитываются коэффициенты их теплопроводности.

4. Процесс вычислений повторяется до тех пор, пока не останется одна биминеральная смесь с коэффициентами теплопроводностей, полученных из теплопроводностей минералов.

5. Суммарный коэффициент теплопроводности этой биминеральной смеси принимается, равным коэффициенту теплопроводности породы.

Для определения теплопроводности биминеральной смеси l_см используется формула, полученная на основе следующих допущений: 1) частицы одного вещества, например, с теплопроводностью l_а имеет форму куба; 2) другое веществе с менее высокой теплопроводностью l_b занимает пространство между частицами вещества и более высокой теплопроводностью; 3) обеспечен достаточно тесный контакт между составляющими биминеральной смеси, который позволяет пренебречь тепловым сопротивлением контакта; 4) тепловой поток перпендикулярен ребру куба. Формула имеет вид:

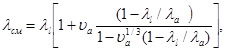(2.3)

где u_а – относительный объем, занимаемый в биминеральной смеси первым веществом.

Расчет по формуле (2.3) осуществляется два раза. Первый раз при условии, когда в качестве первого выбрано вещество с более высокой теплопроводностью, а второго – с меньшим значением теплопроводности (теплопроводности биминеральной смеси l¹_см). Второй раз составляющие биминеральной смеси меняются местами (теплопроводность биминеральной смеси l''_см). Расчетный коэффициент теплопроводности биминеральной смеси находят по формуле:

l_см = nl¢_см + ml¢_см (2.4)

Коэффициенты n и m являются характеристикой горной породы. Их значения для монолитной горной породы принимаются, равными соответственно 0,4 и 0,6.

Реальные горные породы всегда характеризуются определенной пористостью, величина которой может изменяться от долей процентов до 10-15%. Поры оказываются заполненными воздухом (в случае "сухих" пород) или насыщенными влагой. И в первом, и во втором случаях это приводит к снижению теплопроводности породы по сравнению со значениями, характеризующими "абсолютно" плотные породы. На перенос теплоты через воздушные включения, помимо молекулярной составляющей, оказывает влияние излучение и конвекция, которые, в определенной степени, интенсифицируют процесс распространения тепловой энергии. Для установления степени интенсификации процесса теплопереноса вводится так называемое эффективное значение коэффициента теплопроводности. Так, например, при совместном влиянии на теплоперенос молекулярного и лучистого механизмом l_эф составляет:

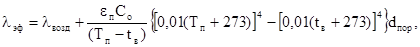(2.5)

где l_возд – коэффициент теплопроводности воздуха, в интервале температур 0-100 °С, l_возд = 0,0244-0,0321 Вт/м×°С; Т_п, t_возд – соответственно температуры пород и воздуха, °С; С_о – коэффициент излучения абсолютно черного тела С_о = 5,7 Вт/м²×К⁴); e_п – приведенная степень черноты поверхностей пор (полостей), между которыми происходит лучистый теплообмен, e_п» 0,45-0,6 (предполагается, что одна из поверхностей находится при температуре пород Т_п, а другая – при температуре воздуха t­_в); d_пар – линейный размер пор (полостей), м.

Расчет суммарной теплопроводности пористой горной породы осуществляется по вышеизложенной методике. При этом воздушные включения с коэффициентом теплопроводности l_эф принимаются за дополнительный "минерал", входящий в состав породы, а коэффициентам n и m в формуле (2.4) присваиваются значения, равные 0,3 и 0,7.

Теплоемкость горной породы численно соответствует количеству теплоты, необходимому для изменения температуры единицы ее массы (объема) на 1°С. Таким образом, теплоемкость породы характеризует способность вещества удерживать или принимать теплоту в процессе охлаждения или нагревания.

Также, как и теплопроводность, теплоемкость горной породы с_п может быть рассчитана как сумма относительных теплоемкостей с_i составляющих ее минералов

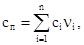(2.6)

где n_i – относительное массовое содержание минерала в породе. В пористой горной породе n_i соответствует значению пористости, а с_i – теплоемкости воздуха.

Удельная теплоемкость каждого из минералов с_i, входящих в состав породы, рассчитывался по формуле

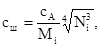(2.7)

где с_А – атомная теплоемкость, равная произведению относительной атомной массы на удельную теплоемкость минерала. Установлено, что с_А практически для всех минералов постоянна и равна 25 Дж/(моль×К).

Температуропроводность горной породы характеризует скорость выравнивания температуры и определяется как отношение теплопроводности к объемной теплоемкости

а_п = l_п/с_пr_п, (2.8)

Теплоусвояемость горной породы характеризует ее теплоаккумуляционные свойства. Величина теплоусвояемости вычисляется по формуле

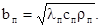(2.9)