Критерий согласия Колмогорова

Критерий согласия Колмогорова предназначен для проверки гипотезы о принадлежности выборки некоторому закону распределения, то есть проверки того, что эмпирическое распределение соответствует предполагаемой модели.

Классический критерий Колмогорова предназначен для проверки простых гипотез. Если проверяется гипотеза о согласии наблюдаемой выборки с законом, все параметры которого известны, то критерий Колмогорова является свободным от распределения: неважно, с каким законом проверяется согласие. Если проверяемая гипотеза справедлива, предельным распределением статистики Колмогорова является распределение Колмогорова .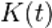

Часто при проверке гипотез о распределении тех или иных данных недостаточно применить какой-то один критерий, в особенности, когда данные наблюдений не показывают значимого отклонения от гипотезы, и ситуация представляется сомнительной.В этих случаях целесообразно воспользоваться другими критериями, основанными на других вероятностных идеях, чтобы при их помощи подвергнуть анализу те же данные. Таким образом, очень важно иметь широкий арсенал методов для статистической обработки данных.

В настоящем параграфе мы кратко опишем два других эффективных подхода, приводящих к хорошим критериям согласия.Критерий Пирсонаможет применяться в самой общей ситуации, являясь весьма универсальным.Его применение особенно оправдано в случае выборок из дискретных распределений.Однако для ряда статистических моделей выводы этого критерия могут быть недостаточно эффективными.

Критерии Колмогорова и Смирнова, о которых идет речь ниже, очень широко применяются в случае непрерывных функций распределения.

Мы ограничимся лишь рассмотрением случая простой гипотезы

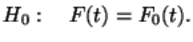
Основой всех методов является рассмотрение некоторой удачно выбранной меры расхождения между выборкой и гипотетическим распределением, а также возможность описать асимптотическое распределение этой меры расхождения при росте объема выборки.В случае критерия Пирсона этой мерой расхождения была функция .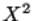

Для критериев Колмогорова и Смирнова выбор меры расхождения связан с эмпирической функцией распределения 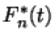(см. Определение 6.1). А именно, рассматривается статистика Колмогорова

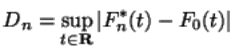
и статистика Смирнова

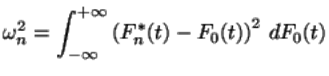
соответственно. Замечательно то, что эти функции легко могут быть вычислены по выборке (не требуется брать какие-либо интегралы, все сводится к простым выражениям, содержащим конечное суммирование и взятие максимума).

Коснемся вопроса об асимптотическом распределении этих функций. Теорема Колмогорова: Если гипотеза 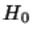верна и 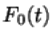непрерывна, то

1. распределение статистики 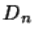является одним и тем же для любой функции распределения 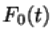и

2. у последовательности 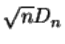существует предельное распределение при .

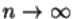Это предельное распределение не совпадает ни с одним упоминавшемся здесь ранее и носит название распределения Колмогорова.

Аналогичное по характеру утверждение имеет место и для статистики Смирнова, а именно, при верной гипотезе 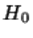и непрерывной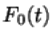

1. распределение 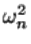зависит только от 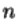и не зависит от ,

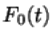2. у последовательности 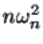существует предельное распределение при .

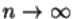Теоремы Колмогорова и Смирнова являются основой для построения соответствующих критериев согласия с критическими множествами вида

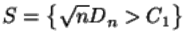и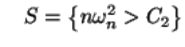

соответственно. Числа 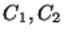определяются по заданным уровням значимости из таблиц допредельных (или предельных, если 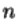очень велико) распределений Колмогорова и Смирнова.Сами эти таблицы могут быть взяты, например, из книги [3].

МЕТОД МОНТЕ-КАРЛО

Метод Монте-Карло (методы Монте-Карло, ММК) — общее название группы численных методов, основанных на получении большого числа реализаций стохастического (случайного) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Используется для решения задач в различных областях физики, химии, математики, экономики,оптимизации, теории управления и др.

Предположим, необходимо взять интеграл от некоторой функции.Воспользуемся неформальным геометрическим описанием интеграла и будем понимать его как площадь под графиком этой функции.

Для определения этой площади можно воспользоваться одним из обычных численных методов интегрирования: разбить отрезок на подотрезки, подсчитать площадь под графиком функции на каждом из них и сложить. Предположим, что для функции, представленной на рисунке ниже, достаточно разбиения на 25 отрезков и, следовательно, вычисления 25 значений функции. Представим теперь, мы имеем дело с 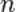-мерной функцией.Тогда нам необходимо 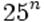отрезков и столько же вычислений значения функции. При размерности функции больше 10 задача становится огромной. Поскольку пространства большой размерности встречаются, в частности, в задачах теории струн, а также многих других физических задачах, где имеются системы со многими степенями свободы, необходимо иметь метод решения, вычислительная сложность которого бы не столь сильно зависела от размерности.Именно таким свойством обладает метод Монте-Карло.