2018-03-09
127
Для анизотропных сред: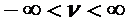 
.
Для ОАКМ (ортотропных тел):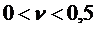 
.
Если такое армирование:
1.
.
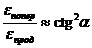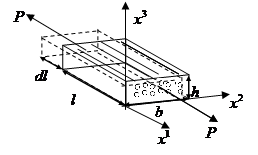
2. 
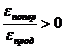. Таким образом при растяжении происходит увеличение размера в поперечном направлении.
У коэффициента Пуассона: первый индекс показывает в каком направлении растягивают, второй индекс показывает направление поперечной деформации.
Я Задача.
Дано: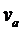 
, 
, 
, 
.
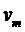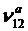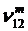Найти: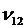 
для однородной среды.
Решение: Как и во 2 задаче делаем предположение: пренебрежение расположения арматуры, и рассматриваем слоистый вариант композита.
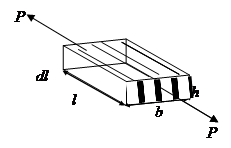
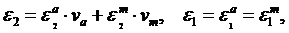
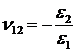(знак минус, т.к. 
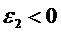, а 
).
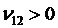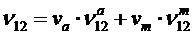- формула смесей для коэффициента Пуассона.
Задача 3а).
Дано: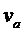 
, 
, 
, 
.
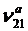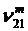Найти: 
.
Решение можно получить двумя способами:
1. аналогично предыдущему (трудный).
2. использование соотношений механики.
для линейно-упругого тела имеет место следующие соотношения:
,
.
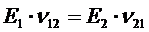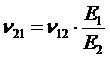Второе соотношение (вытекает из соотношений термодинамики):
.
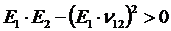4-я Задача. Задача сдвига композита.
Для изотропного тела: 
.
по закону парности 
|
|
|
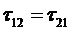
Дано: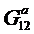 
, 
, 
, 
.
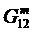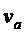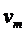Найти: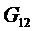 
.
Решение: Вновь используется сильное предположение: пренебрегаем расположением арматуры.
,
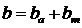
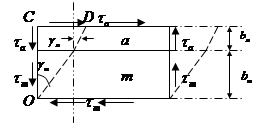где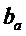 
, 
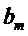- толщина арматуры и матрицы.
Из равновесия тела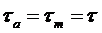 
.
,
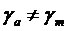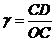- угол сдвига
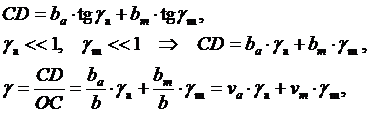
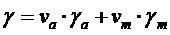- формула смесей для деформаций сдвига
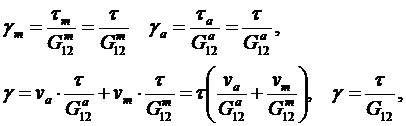
- формула смесей для податливости на сдвиг
Недостатки и достоинства такие же, как для 
.
