Прочностные характеристики КМ

Теплофизические характеристики КМ

5 Задача - Коэффициент линейного температурного расширения поперек волокон .

Дано: , , , .

Найти: .

Решение: Делая предположения задачи 2-4. Т.е. КМ – слоистый.

.

 - закон температурного расширения (закон Дюгамеля-Неймана)

  - формула смесей для .

 

6 Задача. Коэффициент линейного температурного расширения вдоль волокон

Дано: , , , , , .

Найти: .

Решение: Знаем, что

,          (1)

,                (2)

,              (3)

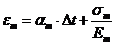.            (4)

,

,                   (4’)

Из (4) и (4’) исключим

Т.к. , то

Примечание:

1. Коэффициент 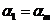, если .
2. Если , то при перепаде температур t одна из фаз будет растягиваться, а другая сжиматься, несмотря на то, что весь образец будет удлиняться. Это следует из соотношения . Если , то матрица будет сжата.

 

Задание 2:

Дано:

Найти: , .

 

 

Прочностные характеристики КМ

Разрушение материала происходит тогда, когда напряжения выходят за пределы некоторой области, ограниченной поверхностью

              (1)

она называется предельной поверхностью (ПП)

Условие (1) называют критерием прочности, теорией прочности.

 

 

Основная задача теории прочности: отыскание формы ПП. Для каждого класса материалов ПП индивидуальна, её аппроксимируют простыми поверхностями после обработки экспериментальных данных.

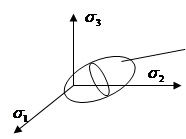
Примеры поверхностей для плоского напряженного состояния , , :

I теория

,

 

 - предел прочности при простом растяжении

Эта теория применяется для чугуна.

IV теория (энергетическая)

.

Эта теория применяется для стали, меди и др. металлов.

 

Для анизотропных тел, даже при аппроксимации квадратичной функции, необходимо найти большое количество неизвестных экспериментальных данных.

Даже если считать материал равнопрочным, то нужно найти 9 const.

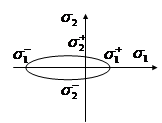Для простоты в дальнейшем рассмотрим только двухосное напряженное состояние.

 

 

        

 

Считаем, что ПП – эллипс.

Будем считать, что поверхность состоит из четырех кусков эллипса достаточно знать 4 точки: , , , .

- предел прочности при растяжении,

- предел прочности при сжатии.

В дальнейшем предполагается, что они известны для каждой фазы КМ.

 

 

1 Задача. Предел прочности при растяжении вдоль арматуры

Дано: , , , .

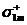Найти:  для КМ.

Решение: Проведем мысленно эксперимент, доведя образец до разрушения.

 

 

Существует два подхода для ответа на этот вопрос:

 - теория хрупкого разрушения;

 - теория вязкого разрушения.

Хрупкое разрушение – разрушение материала путем развития трещины.

Вязкое разрушение – разрушение материала путем сдвига частиц друг относительно друга.

 

 

В 1 подходе считается, что трещина пройдет по всему сечению матрицы и вся нагрузка удерживается к моменту разрушения только арматурой.

 - нижняя оценка предела прочности на растяжения

Эксперименты эту оценку подтверждают не очень хорошо.

Рассмотрим 2 подход, считая, что разрушение идет по сценарию вязкого деформирования.

арматура

матрица

 

Даже после достижении предела прочности арматуры, арматура продолжает работать, в ней напряжения  до тех пор, пока не начнется вязкая деформация в матрице. К моменту разрушения и в матрице мы достигаем предела прочности 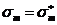. Запишем уравнения равновесия:

 - верхняя оценка предела прочности

Эксперименты лучше подтверждают верхнюю оценку.

Второй подход называется теорией предельного равновесия. Создатель этой теории – Галилей. В XIX веке забыт, благодаря работам Навье, которой ввел расчет по рабочему упругому состоянию. Для стержней впервые переоткрыл в 1914г. Казинчи, а в 1936г. Гвоздев А.А. сформулировал основные теоремы в общем случае. А Прагер, Ходж, Гринберг, Друккер переоткрыли работы Гвоздева в 40 годы XX века.