Большинство материалов (сталь, бетон, полимеры) состоят из частиц, представляющих собой упругие тела, а между собой они соединяются вязкой средой (типа смолы).
|
|
 |
Для упругого элемента принимается закон Гука:
 .
.
Для вязкого элемента в простейшем случае принимается закон Ньютона:
 ,
,
где  - коэффициент вязкости.
- коэффициент вязкости.
Для большинства материалов закон ползучести нелинеен:
например, для стали  ,
,
|
|
Для некоторых материалов такая модель не подходит, т.к. она приводит к выводу, что при бесконечном времени  деформация тоже стремится к бесконечности
деформация тоже стремится к бесконечности  .
.
Файхт придумал такую модель:

Здесь ограничителем для поршня является пружина. Эта модель ущербна тем, что при  :
:  , т.е. закон Гука для тела в целом не удовлетворяется.
, т.е. закон Гука для тела в целом не удовлетворяется.
Модель Кельвина:

Она лучше отражает реологические и упругие свойства материала.
Более сложную многоэтажную модель предложил Ржаницын.
Задача механики КМ заключается в определении коэффициента вязкости  через коэффициенты вязкости арматуры и матрицы:
через коэффициенты вязкости арматуры и матрицы:

Поскольку моделей, состоящих из пружин и вязких элементов, бесконечно, то они были заменены наследственной теорией упругости. Записывается она так:
 - наследственная теория упругости,
- наследственная теория упругости,
где H – ядро ползучести имеет такой вид:


или
Связь напряжений и деформаций можно представить в другом виде:
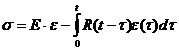 ,
,
где R – оператор, обратный к Н, и называется ядром релаксации.
Основная задача реологии: определение из эксперимента функции R. Наиболее популярными является ядра, которые предложили Абель, Работнов, Ржаницын, Арутюнян.
Для пластиков хорошо подтверждается ядро типа Абеля
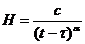 ,
,
где c > 0,  - коэффициенты вязкости.
- коэффициенты вязкости.
Основная задача механики КМ заключается в отыскании функции Н, R для КМ, если известны функции  ,
,  ,
,  ,
,  для матрицы и арматуры.
для матрицы и арматуры.
Примечание: Найти аналитически Н, если известна функция R, очень сложно.
1 Задача. Растяжение вдоль армирования волокон.
Дано:  ,
,  ,
,  ,
,  .
.
Найти:  для КМ.
для КМ.
Решение: Известно, что

 . (1)
. (1)
 определяется по закону смесей:
определяется по закону смесей: 
Запишем соотношение (1) для арматуры и матрицы.
 (2)
(2)
 (3)
(3)
Из 1 Задачи 1 лекции известно, что  . Подставим в эту формулу (2), (3)
. Подставим в эту формулу (2), (3)

Полученное уравнение будет удовлетворяться, если принять, что
 - формула смесей для реологических характеристик вдоль армирования КМ (ядро релаксации).
- формула смесей для реологических характеристик вдоль армирования КМ (ядро релаксации).
2 Задача. Растяжение КМ поперек волокон.
Дано:  ,
,  ,
,  ,
,  .
.
Найти:  для КМ.
для КМ.
 Решение: Напряжение в каждом элементе одинаковы
Решение: Напряжение в каждом элементе одинаковы  а деформация:
а деформация:  . (4)
. (4)
Запишем соотношение для деформаций:
 ,
,
 ,
,
 .
.
Подставляя в формулу смесей (4) получим:
 .
.
Учитывая формулу смесей для податавливости поперек волокон 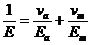 , получим, что
, получим, что  , одно из решений которого:
, одно из решений которого:  - формула смесей.
- формула смесей.
Примечание: Для задачи сдвига соотношение реологии записывается аналогично
 . Аналогично, можно показать, что
. Аналогично, можно показать, что  , т.к.
, т.к.  ,
,  .
.
Задание 3: На железо-бетонную колонну через плиту передается нагрузка P.
 Дано: высота l, площади поперечного сечения стали и бетона
Дано: высота l, площади поперечного сечения стали и бетона  ,
,  ,
,  ,
,  ,
,  ,
, 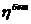 , закон ползучести
, закон ползучести 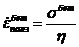 .
.
Найти:  ,
,  .
.
Указание: при  :
:  (для стали и бетона),
(для стали и бетона),
 .
.
 2018-03-09
2018-03-09 297
297









