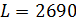Построение последовательных итераций

Получив допустимое исходное базисное решение, перейдем теперь к построению новых базисных решений, улучшающих друг друга: для этого применим метод потенциалов.

Итак, после построения исходного опорного решения все переменные разбиты на две группы: х_jl - базисные и х_ik - свободные; линейная функции стоимости перевозок выразится через свободные переменные так:

(4.4)

Для нахождения коэффициентов при свободных переменных, сопоставим каждому пункту отправления а_i некоторую величину u_i (i =1, 2,..., p), которую назовем потенциалом пункта а_i, и каждому пункту назначения b_k величину v_k - потенциал пункта b_k. Свяжем эти величины равенством

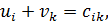
(4.5)

где 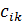- стоимость перевозки одной единицы груза из пункта а_i в пункт b_k.

Доказано, что совокупность уравнений (4.5), составленных для всех базисных переменных, является совместной системой линейных уравнений, причем значение одной из переменных можно задавать произвольно, и тогда значения остальных переменных находятся из системы однозначно.

Обозначим для свободных переменных сумму соответствующих потенциалов через , т.е.

(4.6)

и назовем ее косвенной стоимостью (в отличие от данной стоимости 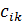). Тогда коэффициенты при свободных переменных в соотношении (4.4) определяются с помощью равенства

(4.7)

Если значения всех величин неотрицательны, то исходное решение является оптимальным. Если же среди них имеются отрицательные, то переходим к следующему базису путем перемещения перевозки в клетку, где величина 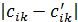максимальна.

Перемещение производится так, что по отношению к выбранной клетке образуется замкнутая ломаная, называемая циклом пересчета. Одна из вершин цикла находится в выбранной свободной клетке, другие – в заполненных. В каждой вершине ломаной встречаются два звена, одно из которых располагается по строке, другое – по столбцу. Далее каждой клетке в цикле поочередно присваиваются знаки «+» и «-», начиная со свободной. Перевозка, перемещаемая по циклу, равна минимуму среди клеток со знаком «-».

Иногда перевозка, перемещаемая по циклу, может оказаться равной нулю. В таком случае по циклу передается нулевая перевозка, и тогда свободная клетка становится занятой нулевой перевозкой, а клетка с нулевой перевозкой – свободной. Если при перемещении перевозки по циклу образуется нуль сразу в нескольких заполненных клетках, то свободной из них следует считать только одну (любую), остальные клетки (из обнулившихся) следует считать заполненными нулевой перевозкой.

Таким образом, правила вычислений по методу потенциалов сводятся к следующему:

1. Находят потенциалы u_i и v_k всех пунктов отправления а_i и потребления b_k на основе равенства (4.5).

2. Полученный план перевозок считают оптимальным, если для всех свободных переменных (клеток) выполняется условие

. (4.8)

3. Если план неоптимальный, то выбирают свободную переменную, для которой величина 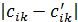максимальна, это соответствует элементу с наибольшим отрицательным коэффициентом при свободной переменной в правой части функции L.

4. Для выбранной в п.3 переменной находят соответствующий ей цикл пересчета и производят перемещение по этому циклу. Это перемещение приводит к новому допустимому решению.

5. Вышеуказанные операции 1-4 повторяют до тех пор, пока не получат оптимальный базис, т.е. неотрицательные коэффициенты при свободных переменных в правой части линейной функции L.

Планирование объемов перевозок

Три шахты поставляют на обогатительные фабрики уголь одной марки. Объем суточной добычи шахт, суточная мощность фабрик и стоимость транспортирования 1 т угля представлены в таблице 4.2.

Таблица 4.2

Исходные данные
Шахты	Фабрики				Добыча
Шахты	1	2	3	4	Добыча
1	3	5	6	2	170
2	6	4	7	5	250
3	5	4	6	5	180
Мощность	150	230	160	60	600

Требуется составить такой план перевозок, чтобы обеспечить минимум общей суммы транспортных расходов.

Аналитический метод решения

Данная задача закрытого типа, так как сумма запасов равна сумме спроса:

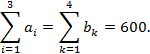
Целевая функция будет иметь следующий вид:

Построим допустимое исходное базисное решение по методу северо-западного угла (табл.4.3).

Таблица 4.3

Базисное решение. Целевая функция
Шахты	Фабрики				Добыча
	1	2	3	4

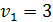
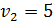
1	3 150	- 5 20	6 8	+ 2 7	170
2	6 2	+ 4 210	- 7 40	5 6	250
3	5 1	4 3	+ 6 120	- 5 60	180
Мощность	150	230	160	60	600

На основе равенства (4.5) составим систему для вычисления потенциалов и :

Присвоим первому поставщику потенциал . Тогда 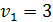, , 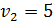, , . Найденные значения потенциалов и значения величин запишем в таблицу 4.3 с исходным базисным решением

Проверим имеющийся план перевозок на оптимальность с помощью условия (4.8). Для удобства запишем в виде матрицы

Очевидно, что исходное решение не является оптимальным, так как среди имеются отрицательные. Для улучшения плана необходимо переместить перевозку в клетку, где разность 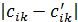максимальна, т.е. в клетку (1;4). Пометим ее знаком «+» и построим для нее цикл пересчета. В клетках со знаком «-» минимальное число перевозок равно 20. Это число и перемещаем по циклу. Результат заносим в новую таблицу 4.4.

Таблица 4.4

Итерация 1. Целевая функция
Шахты	Фабрики				Добыча
	1	2	3	4

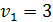
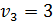
1	- 3 150	5 0	6 3	+ 2 20	170
2	6 7	4 230	7 20	5 6	250
3	+ 5 6	4 3	6 140	- 5 40	180
Мощность	150	230	160	60	600

Матрица коэффициентов

Здесь также имеются отрицательные элементы. Поскольку все они равны, то выберем одну из клеток с меньшей стоимостью перевозки. Например, клетку (3;1), и составим для нее цикл пересчета. Результаты в табл. 4.5.

Таблица 4.5

Итерация 2. Целевая функция
Шахты	Фабрики				Добыча
	1	2	3	4

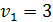
1	3 110	5 1	6 4	2 60	170
2	6 6	4 230	7 20	5 5	250
3	5 40	4 3	6 140	5 4	180
Мощность	150	230	160	60	600

Матрица коэффициентов

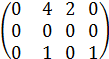В матрице оценок для последней итерации нет отрицательных элементов. Это значит, что полученное распределение перевозок оптимальное.

Построим допустимое исходное базисное решение по методу минимальной стоимости и рассчитаем потенциалы (табл.4.6).

Таблица 4.6

Базисное решение. Целевая функция
Шахты	Фабрики				Добыча
	1	2	3	4

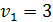
1	3 110	5 2	6 5	2 60	170
2	6 5	+ 4 90	- 7 160	5 4	250
3	5 40	- 4 140	+ 6 7	5 4	180
Мощность	150	230	160	60	600

Матрица коэффициентов

Здесь только один отрицательный элемент в клетке (3;3). Нетрудно видеть, что после перемещения перевозок по циклу, получится то же самое решение, которое было получено выше (табл.4.5).

Метод решения средствами Excel

Оптимальный план перевозок в табличном процессоре Excel найдем также с помощью надстройки «Поиск решения». Главное отличие этого метода в том, что не нужно находить базисное решение.

1. Для выполнения расчетов создадим две отдельных матрицы (рис.4.1). В ячейках B4:E6 будет отображаться искомый план перевозок, а в ячейках B13:E15 запишем стоимости перевозок .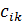

2. В ячейки F4:F6 запишем условия (4.1).

3. В ячейки G4:G6 запишем значения объемов добычи.

4. В ячейки B7:E7 запишем условия (4.2).

5. В ячейки B8:E8 запишем значения мощностей.

6. В ячейку F8 запишем сумму мощностей обогатительных фабрик. В ячейку G7 – сумму объемов суточной добычи шахт. Равенство значений подтверждает, что данная задача закрытого типа.

7. В ячейку F11 запишем целевую функцию

=СУММПРОИЗВ(B4:E6;B13:E15)

Рис.4.1. Исходный вид транспортной задачи с формулами

8. Далее открываем диалоговое окно Поиск решения (рис.4.2), в котором указываем необходимые параметры. Чтобы значение целевой функции было минимальным, установим переключатель в положение Минимум. В поле Изменяя ячейки переменных вводим матрицу плана перевозок. В следующем поле указываем соответствующие ограничения. В поле Выберите метод решения можно выбрать или нелинейный метод обобщенного понижающего градиента (ОПГ) или симплекс-метод. Так как наша задача относится к линейным, то выбираем метод решения симплекс-методом и нажимаем кнопку Найти решение.

Рис.4.2. Параметры поиска решения транспортной задачи

9. После окончания работы программы откроется окно результатов, в котором будет предложено сохранить результат или вернуться в предыдущее окно.

Рис.4.3. Решение симплекс-методом

При выборе симплекс-метода получаем план, который отличается от того, который был получен аналитическим методом, но также отвечающий условиям оптимальности (рис.4.3). При выборе метода ОПГ получим решение, которое совпадает с аналитическим решением (рис.4.4). В обоих случаях минимальные транспортные издержки составят 2550 денежных единиц, что на 5% меньше, чем по базисному плану.

Рис.4.4. Решение по методу ОПГ

Часто при решении горно-экономических задач встречается ограничение пропускной способности маршрутов, особенно при синтезе горных выработок. Предположим, что по маршруту 2-2 можно перевезти не более 100 т. В этом случае решение задачи с помощью Excel легко получить, добавив дополнительное ограничение, что значение в ячейке С5 меньше или равно 100. Полученное при этом условии решение (рис.4.5) отличается возросшей величиной транспортных издержек. Это подтверждает важный принцип оптимизации: дополнительные ограничения, влекущие за собой изменение плана, всегда приводят к ухудшению оптимального решения задачи. Это же касается и случаев волевого принятия решений типа обязательных поставок.