ДИ и ДВ для случайных величин в предположении нормального распределения

Так как функция Лапласа нечетная, то равенство (5.9) будет иметь вид:

             (5.10)

Из уравнения

                                         (5.11)

находим значение :

                              (5.12)

где  – функция, обратная функции Лапласа. Величина  выражается через неизвестную нам дисперсию  по формуле (5.7). Поэтому в качестве ориентировочного значения  взять оценку  и положить приближенно .

Теперь доверительный интервал выражается величиной:

где  определяется по формуле (5.12),

β - заданный уровень доверительной вероятности.

Методика расчета доверительного интервала с помощью функции

Лапласа

1. В каждой точке, где имеются данные об n опытах, находим оценки

 – для математического ожидания;

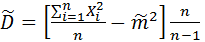– для дисперсии,

– для среднеквадратического отклонения.

2. Задаемся уровнем доверительной вероятности

3. Вычисляем отклонение  по формуле

.

4. Границы доверительного интервала определяем по формуле

.

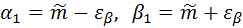5. В качестве ошибки в определении среднего значения O_ш можно принять отношение максимального отклонения  к математическому ожиданию :
                               (5.13)

Для практических целей последнюю формулу можно преобразовать, выразив относительную ошибку через коэффициент вариации . Т.к.  , то отностительная ошибка 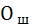примет следующее выражение:

Отношение может быть принято в качестве оценки коэффициента вариации.

Тогда                          (5.14)

Итак, относительная ошибка  в определении среднего значения зависит в такой постановке задачи от коэффициента вариации , числа опытов n и доверительной вероятности .

Соотношение 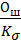= =  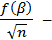это доля ошибки от коэффициента вариации. Она зависит только от принятого уровня доверительной вероятности β и числа опытов n.

График функции =  строится по табличным значениям обратной функции Лапласа, он приведен на рис. 5.8.