Практическая работа № 11

Тема: Исследование рядов на сходимость

Цель: закрепить понятие числового ряда, сходимость ряда и умения определять сходимость ряда, используя признак Даламбера; закрепить понятие знакопеременного ряда и умение использовать признак Лейбница для определения сходимости ряда

 

Методические указания к выполнению практической работы

1. Повторите признак сходимости Даламбера; рассмотрите примеры применения; выполните задание № 1

2. Повторите признак сходимости Лейбница; рассмотрите примеры применения; выполните задание № 2

3. Подберите признак сходимости для выполнения задания № 3

 

Определение 1. Пусть задана числовая последовательность a_n, nЄN. Тогда выражение a₁+a₂+…+a_n+… (1)

называется числовым рядом и обозначается

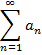
Следовательно,

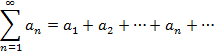
Числа a₁, a₂, … называются членами ряда (первым, вторым и т.д.), a_n – называется n-м или общим членом ряда.

Если будем последовательно складывать члены ряда S₁=a₁, S₂=a₁+ a₂, S₃=a₁+a₂+a₃, …, S_n=a₁+a₂+…+a_n, …, то S₁, S₂, …, S_n, … называются частичными суммами ряда.

Теорема 1. (необходимое условие сходимости ряда) Если ряд с общим членом a_n сходится, то a_n →0 при n →∞.

 

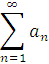Пусть дан ряд                    , a_n ≥0.

 

Теорема 2. (признак Даламбера) Пусть для ряда с положительными членами a_n выполняется условие

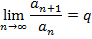
Тогда если q<1, то ряд сходится, а если q>1, то ряд расходится.

Примеры выполнения задания

Пример 1. Сходится ли ряд?

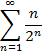
Решение:

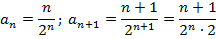
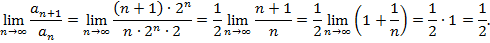
Следовательно, ряд сходится.

Пример 2. Сходится ли ряд?

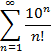
Решение:

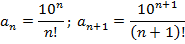
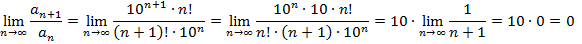
Следовательно, ряд сходится.

 

Признак Лейбница

Важный класс сходящихся рядов образуют так называемые абсолютно сходящиеся ряды.

Теорема 3. Если ряд

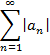
сходится, то и ряд

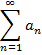
сходится.

Определение 2. Ряд

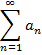
называется абсолютно сходящимся, если сходится ряд

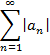
       Теорема 4. утверждает, что если ряд абсолютно сходится, то он и просто сходится.

Для исследования рядов на абсолютную сходимость можно пользоваться всеми признаками сходимости для рядов с неотрицательными членами.

Теорема 5. Пусть для ряда

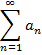
выполняется условие

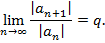
Тогда если q<1, то ряд сходится абсолютно, а если q>1, то ряд расходится.

       Теорема 6. (признак Лейбница) Если последовательность (a_n) из положительных чисел убывает и

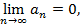
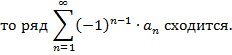
Из признака Лейбница следует, что ряд

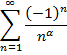
сходится при любом α>0. Однако он не является абсолютно сходящимся, если 0<α≤1.
       Определение 3. Ряд называется условно сходящимся, если он является сходящимся, но не является абсолютно сходящимся.