Вариационные ряды и их характеристики

Первичная обработка результатов

Наблюдений

Информация о работе любой отрасли производственной сферы (до- быча нефти и газа, ремонт скважин, нефтехимическое производство, ма- шиностроение и т.д.) ставит перед ее руководством и наукой задачу: как, сведя к минимуму расходы по использованию природных, материальных и людских ресурсов, эффективно анализировать работу отрасли, управлять ею, прогнозировать развитие возможных сценариев поведения отрасли как сложной системы. Это означает, что математическому моделированию подлежит (дискретный, непрерывный, фрактальный) информационный по-

ток — статистическая совокупность — в виде случайных событий и слу- чайных величин. Изучение подобного рода массовых явлений, выявление их статических и динамических закономерностей становится предметом математической статистики. Среди полезной информации о статистиче- ской совокупности особый интерес представляют статистические дан- ные, которые можно записать в виде ряда { x ⁽¹⁾, x ⁽²⁾, …, x ⁽ⁿ⁾} числовых зна- чений интересующего нас признака (случайной величины Х). Обработку этого ряда производят посредством методов математической статистики; при этом точность статистических методов повышается с ростом n.

Пусть A — некоторое множество (например, множество всех жите- лей данного города), B Ì A — случайно выбранное подмножество (напри- мер, множество случайно выбранных жителей, при этом некий наблюда- тель измерил у них рост, скажем, в сантиметрах). Выборочным методом называется метод исследования общих свойств множества А на основе изучения так называемых статистических свойств лишь множества В. Множество А называется генеральной совокупностью, а множество В — выборочной совокупностью или выборкой. Число N = | A | элементов мно- жества А называется объемом генеральной совокупности, а число n = | B |

— объемом выборки. При изучении некоторого признака Х (в нашем при- мере — роста) выборки производят испытания или наблюдения (измере- ние роста).

Пусть в результате независимых испытаний, проведенных в одина- ковых условиях, получены числовые значения { x ⁽¹⁾, x ⁽²⁾, …, x ⁽ⁿ⁾}, где n — объем выборки.

При обработке статистических данных строятся статистики. Стати- стикой называется функция

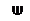
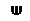R n ¾¾ f ® R

(x ⁽¹⁾, x ⁽²⁾, …, x ⁽ⁿ⁾) = х a f (x),

которая набору значений

(x (1), x (2) ,..., x (n) )

случайной величины ставит в

соответствие по некоторому правилу f действительное число. Статистика является числовой функцией на множестве реализаций случайной величи- ны.

Значения х ⁽ⁱ⁾ располагают в порядке возрастания:

x 1,

x 2,..., xn

(x 1 <

x 2 <... <

xn).

Может оказаться, что некоторые варианты х_i в выборке встречаются не- сколько раз.

Число n_i, показывающее, сколько раз встречается варианта х_i в выбо- рочной совокупности, называется ее частотой (эмпирической частотой).

Частоты вариант называются их весами. Отношение w_i = n_i / n частоты n_i к объему n выборки называют относительной частотой (частостью) вари- анты х_i.

Вариационным рядом (или статистическим распределением) назы- вается ранжированный в порядке возрастания или убывания ряд вариант с соответствующими им весами.

Различают дискретные и непрерывные вариационные ряды. Дис- кретный вариационный ряд записывают в виде табл. 1.

Т а бл и ца 1

Варианты, x_i	x ₁	x ₂	...	x_k
Частоты, n_i	n ₁	n ₂	...	n_k

Здесь n_i — частота появления значения x_i, причем å ni

i =1

= n.

Если объем n выборки большой (n > 30), то результаты наблюдений сводят в интервальный вариационный ряд, который формируется следую- щим образом.

Вычисляют размах R варьирования признака Х, как разность между

наибольшим

x max

и наименьшим

x min

значениями признака:

R = x max - x min.

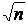Размах R варьирования признака Х делится на k равных частей и таким об- разом определяется число столбцов (интервалов) в таблице. Число k час- тичных интервалов выбирают, пользуясь одним из следующих правил:

1) 6 £ k £ 20,

2) k»,

3) k» 1 + log2 n» 1 + 3,221× lg n.

При небольшом объеме n выборки число k интервалов принимают равным от 6 до 10. Длина h каждого частичного интервала определяется по формуле: h = R / k.

Величину h обычно округляют до некоторого значения d. Например,

если результаты xi

признака Х — целые числа, то h округляют до целого

значения, если xi

содержат десятичные знаки, то h округляют до значения

d, содержащего такое же число десятичных знаков. Затем подсчитывается

частота n_i, с которой попадают значения xi

признака Х в i -й интервал.

Значение

xi, которое попадает на границу интервала, относят к какому-

либо определенному концу, например, к левому. За начало

x 0 первого ин-

тервала рекомендуется брать величину

x 0 = x min

- 0,5 h. Конец xk

послед-

него интервала находят по формуле

xk = x max + 0,5 h. Сформированный

интервальный вариационный ряд записывают в виде табл. 2.

Таблица 2

Варианты-интервалы, (xi -1; xi)	(x 0; x 1)	(x 1; x 2)	...	(xk -1; xk)
частоты, n_i	n ₁	n ₂	...	n_k

Интервальный вариационный ряд изображают в виде гистограммы частот n_i или гистограммы относительных частот w_i = n_i / n.

Гистограммой называется ступенчатая фигура, для построения ко-

торой по оси абсцисс откладывают отрезки, изображающие частичные ин-

тервалы (xi -1; xi ) варьирования признака Х, и на этих отрезках, как на ос-

нованиях, строят прямоугольники с высотами, равными частотам или час- тостям соответствующих интервалов.

Для расчета статистик (выборочной средней, выборочной диспер- сии, асимметрии и эксцесса) переходят от интервального вариационного

ряда к дискретному. В качестве вариант xi

этого ряда берут середины ин-

тервалов (xi; xi +1). Дискретный вариационный ряд записывается в виде

табл. 3 или табл. 4.

Т а бл и ца 3

Варианты, х_i	х ₁	х ₂	...	х_k
частоты, n_i	n ₁	n₂	...	n_k

Здесь å ni = n, где n — объем выборки.

Т а бл и ца 4

Варианты, xi	x 1	x 2	...	xk
относительные час- тоты, w_i = n_i / n	w ₁	w ₂	...	w_k

Здесь å wi

i =1

= 1.

Графически дискретный вариационный ряд изображают в виде поли- гона частот (соответственно в виде полигона относительных частот) сле- дующим образом. Сначала на числовой плоскости строят точки (xi; n_i)

(точки (xi; w_i)), где xi

— i -я варианта, число n_i (число w_i) называют час-

тотой (частостью). Затем строят ломаную, соединяющую построенные точки, которую и называют полигоном.

Вариационные ряды графически можно изобразить в виде кумуля- тивной кривой (кривой сумм — кумуляты). При построении кумуляты дискретного вариационного ряда на оси абсцисс откладывают варианты

xi, а по оси ординат соответствующие им накопленные частоты Wi. Со-

единяя точки (xi; Wi) отрезками, получаем ломаную, которую называют

кумулятой. Для получения накопленных частот и дальнейшего построения точек (xi; Wi) составляется расчетная табл. 5.

Т а бл и ца 5

Варианты, xi	x 1	x 2	...	xk
Относительные частоты, w_i = n_i / n	w ₁ = n ₁ / n	w ₂ = n ₂ / n	...	w_k = n_k / n
Накопленные относительные частоты, W_i = W_i _– ₁ + w_i	W ₁ = w ₁	W ₂ = W ₁ + w ₂	...	Wk = Wk – 1 + wk

При построении кумуляты интервального вариационного ряда лево- му концу первого интервала сопоставляется частота, равная нулю, а пра- вому — частота этого интервала. Правому концу второго интервала соот- ветствует накопленная частота первых двух интервалов, то есть сумма час- тот этих интервалов и т. д. Правая граница последнего интервала равна сумме всех частот, то есть объему n выборки.

Для характеристики свойств статистического распределения в мате- матической статистике вводится понятие эмпирической функции распре- деления.

Эмпирической функцией распределения или функцией распределения

называется функция F _в (x), определяемая равенством:

F _в (x) = nx , (1)

где n — объем выборки, n_x — число вариант

xi, меньших х.

Эмпирическая функция F _в (x) служит для оценки теоретической функции распределения генеральной совокупности. Различие между ними состоит в том, что теоретическая функция F (x) определяет вероятность со- бытия X < x, а эмпирическая функция F _в (x) определяет относительную частоту этого события. Из теоремы Бернулли следует, что при больших n числа F _в (x) и F (x) мало отличаются одно от другого в том смысле, что

lim P [ | F (x) – F _в (x) | < e] = 1 (e > 0).

n ®¥

Другими словами, при больших объемах выборки n, согласно закону больших чисел, функция F _в (x) сходится по вероятности к теоретической функции F _в (x) признака Х.

Аналогом этой функции в теории вероятностей является интеграль- ная функция распределения F (x). Функция F _в (x) отличается от функции F

(x) тем, что вместо вероятности P (X < x) берется накопленная частота

Wi = nx. Значение функции F _в (x) равно числу n_x принятых признаком Х

вариант, меньших х, деленному на объем n выборки.

Эмпирическая функция F _в(x) служит для оценки теоретической функции распределения генеральной совокупности.

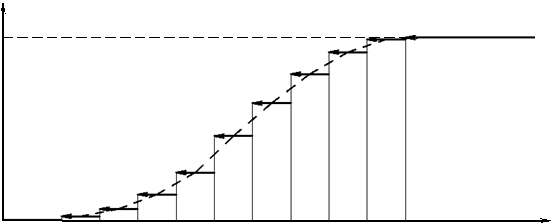
Значения эмпирической функции F _в(x) принадлежат промежутку

[0; 1]; ее графиком служит кусочно-постоянная кривая (рис. 1). Она имеет

скачки в точках, которые соответствуют вариантам

xi. При обработке ре-

F _в (x)

x 1 x 2 x 3

xi xn x

Рис. 1. Кумулята и эмпирическая функция распределения.

зультатов эксперимента, например, результатов механических испытаний, целесообразно вместо ступенчатой кривой вычерчивать плавную кривую (на рис. 1 это штриховая линия), которая проходит через точки, располо- женные посередине вертикальных частей ступенчатой кривой [11]. Абс-

циссами этих точек служат значения механической характеристики

xi, а

ординатами — эмпирическая функция F _в (x), характеризующая оценку ве-

роятности события Х £ хi.

§ 2. Расчет выборочных характеристик статистического распределения

Рассмотрим выборку объема n со значениями

x 1,

x 2,..., xn

призна-

ка Х. Для характеристики важнейших свойств статистического распреде- ления используют средние показатели, называемые выборочными число-

выми характеристиками. Если значения xi

признака Х не сгруппированы

в вариационные ряды (табл. 2, 3, 4) и объем выборки n небольшой, то

оценки для неизвестных математического ожидания а и дисперсии ходят по формулам:

s2 на-

x = 1 å xi

(2)

i =1

для математического ожидания и

S 2 = 1 å(x - x)2

= 1 å x 2 - x 2

(3)

i =1

n i

i =1

для дисперсии [8].

Если результаты наблюдений сгруппированы в дискретный вариаци- онный ряд (табл. 3), то те же оценки находят по формулам:

x = å x n , i i

k k

1 n = å ni , (4)

i =1

k n

S 2 = 1 å(xi - x)2 ni = 1 å n x 2 - x 2. (5)

i =1

n i i

i =1

Несомненно, что формулы (2) и (4), как и (3) и (5) дают одинаковые результаты соответственно для x и S ².

По формуле (5) вычисляют

S 2 в случае, если объем выборки

n ³ 50.

Если же

n < 50, то вычисляют исправленную дисперсию

S €2 по формуле:

S = å (x

ˆ 2 1

n -1

i =1

- x) 2

(6)

для простой выборки, или

S ˆ2 = 1 å(x - x)2 n

(7)

n -1 i i i =1

для взвешенной выборки.

Выборочное среднее квадратическое отклонение находят по форму-

лам

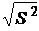S = или

S ˆ = (8)

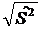при различных объемах выборки.

Для анализа вариационных рядов вычисляют такие статистики, как моду и медиану.

Модой

M o X

называют варианту, которая имеет наибольшую часто-

ту. Например, для вариационного ряда

x_i	4	9	14	19
n_i	3	7	2	5

мода равна

M o X

= 9.

Медианой

Me X

называют варианту, которая делит вариационный

ряд на равные по числу вариант части [2].

При нечетном объеме выборки Например, для вариационного ряда

n = 2 k + 1 медиана равна

M e X

= xk +1.

x_i	3	5	8	12	15
n_i	6	2	4	5	8

медиана равна M e X = x 13 = 12.

При четном объеме выборки

n = 2 k

медиана находится по формуле:

Me X

= xk + xk +1 . (9)

Здесь xk

— варианта, которая находится слева от середины вариа-

ционного ряда, а ционного ряда:

xk +1

— справа от нее. Например, для следующего вариа-

x_i	2	5	7	10	12	14
n_i	3	4	8	2	3	6

медиана равна

M e X

= 7.

Для вычисления выборочной средней x, выборочной дисперсии

S 2,

асимметрии As и эксцесса Ex при достаточно большом объеме выборки

(n > 30) применяют метод произведений [3]. При этом вводят условные варианты u_i, которые вычисляют по формуле:

u = xi - C , (10)

где C = M_o X, h — шаг (длина интервала).

Составляется расчетная табл. 6.

Т а бл и ца 6

xi	ni	ui	niui	niu ² i	niu ³ i	niu ⁴ i	контрольный столбец ni (ui +1)²

строка сумм:	S =	S =	S =	S =	S =	S =	S =

Контроль вычислений ведут по формуле:

å ni + 2å niui + å n u 2 = å ni (ui + 1)2.

Пользуясь табл. 6, вычисляют [3] условные начальные моменты по формулам:

M * = 1 å n u

, (11)

1 n i i

M * = 1 å n u 2, (12)

2 n i i

M * = 1 å n u 3 , (13)

3 n i i

M * = 1 å n u 4. (14)

4 n i i

Тогда выборочную среднюю находят по формуле:

x = M * h + C. (15)

Выборочную дисперсию находят по формуле:

S 2 = (M * - M *2) h 2 . (16)

2 1

Выборочное среднее квадратическое отклонение находят по форму-

ле:

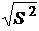S = . (17)

Асимметрию и эксцесс находят по формулам:

s 3

A = m 3 , (18)

E = m 4 - 3, (19)

S 4

где

m 3 = (M * - 3 M * M * + 2 M * 3) h 3

(20)

3 2 1 1

— условный центральный момент третьего порядка, а

m 4 = (M * - 4 M * M * + 6 M * M *2 - 3 M *4 ) h 4

(21)

— условный центральный момент четвертого порядка.

Для характеристики колеблемости признака Х используют [2] отно- сительный показатель — коэффициент вариации V, который для положи- тельной случайной величины Х вычисляют по формуле:

V = S / x. (22)