2018-03-09
116
| Федеральное агентство морского и речного транспорта | |
| Федеральное государственное образовательное учреждение высшего профессионального образования | |
| Государственная морская академия | |
|
КАФЕДРА ПРИКЛАДНОЙ МЕХАНИКИ И ИНЖЕНЕРНОЙ ГРАФИКИ Отчет
о выполнении расчетно-графической работы на тему
РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛОК | |
| Выполнил: | |
| Проверил: | |
|
Санкт-Петербург 200 г. | |
| СН | |
| РС | |
| ЭQ | |
| ЭM | |
Рис. 1. Схема нагружения балки № … задания А.
Эпюры Q и М
Исходные данные задания А: а =… м; b = …м; с = …м.
; 
; 
;
[s] = 140 МПа.
Профиль: .
ЗАДАЧА I. Построение эпюр Q и М
1. Определяем значения сил реакций опор RA и RB из уравнений статики равновесия моментов и их действительное направление:
………………………………………………………………………………= 0;
………………………………………………………………………………= 0;
Проверка:
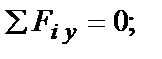…………….………… = …………………………………….= 0;
0 = 0 – тождество!
2. Выполняем расчет Q в поперечных сечениях балки и построение графика-эпюры ЭQ по схеме, форма которой приведена на с. 14.
Аналитическое выражение для Q в общем виде для первого участка балки:
кН.
Рассчитываем Q в левом крайнем сечении первого участка Q 1 и правом крайнем Q 2:
кН;
кН.
Аналитическое выражение для Q в общем виде для второго участка:
кН.
Находим 
в левом крайнем сечении второго участка Q 3 и правом крайнем Q 4:
кН;
(кН).
Аналитическое выражение для Q в общем виде для третьего участка:
кН.
Определяем Q в левом крайнем сечении третьего участка Q 5 и правом крайнем Q 6:
кН;
кН.
По рассчитанным значениям Q 1, Q 2, Q 3, Q 4, Q 5, Q 6 строим ЭQ
на рис. 1.
3. Выполняем расчёт M в поперечных сечениях балки и построение графика-эпюры ЭМ.
Аналитическое выражение для М в общем виде для первого участка балки:
кН×м.
Рассчитываем М в левом крайнем сечении первого участка (М 1) и правом (М 2):
кН×м;
кН×м;
Аналитическое выражение для М в общем виде для второго участка:
кН×м.
Находим М в левом крайнем сечении второго участка М 3 и правом М 4:
кН×м;
кН×м;
Аналитическое выражение для М в общем виде для третьего участка:
кН×м.
Определяем М в левом крайнем сечении третьего участка М 5 и правом М 6:
кН×м;
кН×м;
По рассчитанным значениям М 1, М 2, М 3, М 4, М 5, М 6 строим ЭМ на рис. 1.
Пользуясь зависимостями, вытекающими из формулы (11), проверяем правильность построения эпюр Q и M.
ЗАДАЧА II. Подбор профиля балки
;
………………. (м3) 
(см3).
Перегрузка:
Недогрузка:
Из сортамента: 
см3
Номер профиля № ….………
| СН | |
| РС | |
| ЭQ | |
| ЭM | |
Рис. 2. Схема нагружения балки № … задания Б.
Эпюры Q и М
Исходные данные задания Б: а =… м; b = …м; с = …м.
; 
; 
; 
.
Профиль: .
ЗАДАЧА I. Построение эпюр Q и М
1. Определяем значения сил реакций опор RA и RB из уравнений статики равновесия моментов и их действительное направление:
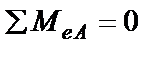; ………………………………………………………………………………= 0;
; ………………………………………………………………………………= 0;
Проверка:
; …………….………… = ……………………………..= 0; Þ 0 = 0 – тождество!
2. Выполняем расчёт Q в поперечных сечениях балки и построение графика-эпюры ЭQ.
Уравнение для первого участка балки:
кН.
Рассчитываем Q в левом крайнем сечении первого участка Q 1 и правом – Q 2:
кН;
кН.
Уравнение для второго участка:
кН.
Находим Q в левом крайнем сечении второго участка Q 3 и правом Q 4:
кН;
кН.
Уравнение для третьего участка:
.кН.
Определяем Q в левом крайнем сечении третьего участка Q 5 и правом Q 6:
кН;
кН.
По рассчитанным значениям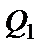 
, 
, 
, 
, 
, 
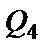строим ЭQ
на рис. 2.
3. Выполняем расчёт М в поперечных сечениях балки и построение графика-эпюры ЭМ.
Уравнение для первого участка балки:
кН×м.
Рассчитываем М в левом крайнем сечении первого участка (М 1) и правом – (М 2):
кН×м;
кН×м;
Уравнение для второго участка балки:
кН×м.
Находим М в левом крайнем сечении второго участка (М 3) и правом – (М 4):
кН×м;
кН×м;
Уравнение для третьего участка балки:
кН×м.
Определяем М в левом крайнем сечении третьего участка (М 5) и правом – (М 6):
кН×м;
кН×м;
По рассчитанным значениям 
, 
, 
, 
, 
, 
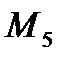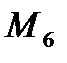строим ЭМ на рис. 2.
На участках со сплошной нагрузкой парабола эпюры М строится по трём точкам: двум крайним значениям М расчетного участка и в середине участка, если нет вершины параболы. Если имеется вершина параболы, то третья точка – её значение:
…………………………………………………………………………………
…………………………………………………………………………………
…………………………………………………………………………………
…………………………………………………………………………………
…………………………………………………………………………………
Проверяем правильность построения эпюр Q и M на основании теоремы Журавского.
ЗАДАЧА II. Расчёт площади А поперечного сечениябалки
м3 
см3.
………………………………………………………………………………
………………………………………………………………………………
см2.
ВЫВОД
Приложение 2
