| Выражения вида a 2−ab+b 2 и a 2+ab+b 2 называют соответственно неполным квадратом разности и неполным квадратом суммы (сравните их с квадратом разности и квадратом суммы). a 2−2ab+b 2 и a 2+2ab+b 2 |
| При любых значениях a и b верно равенство (a+b)(a 2−ab+b 2) = a 3+b 3. (1) Доказательство. (a+b)(a 2−ab+b 2) = = a 3+a 2b−a 2b−ab 2+ab 2+b 3 = = a 3+b 3 Так как равенство (1) верно при любых значениях a и b, то оно является тождеством. Это тождество называется формулой суммы кубов. Если в эту формулу вместо a и b подставить какие-нибудь выражения, например 2x и y 2, то опять получится тождество. (2x+y 2)(4x 2−2xy 2+y 4) = 8x 3+y 6. Поэтому формула суммы кубов читается так: произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений. |
| При любых значениях a и b верно равенство (a−b)(a 2+ab+b 2) = a 3−b 3. (2) Доказательство. (a−b)(a 2+ab+b 2) = = a 3−a 2b+a 2b−ab 2+ab 2−b 3 = = a 3−b 3 Так как равенство (2) верно при любых значениях a и b, то оно является тождеством. Это тождество называется формулой разности кубов. Если в эту формулу вместо a и b подставить какие-нибудь выражения, например 2x и y 2, то опять получится тождество. (2x−y 2)(4x 2+2xy 2+y 4) = 8x 3−y 6. Поэтому формула разности кубов читается так: произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений. |
28,29 Куб суммы и куб разности. Правила
| При любых значениях a и b верно равенство (a+b) 3 = a 3+3a 2b+3ab 2+b 3. (1) Доказательство. (a+b) 3 = (a+b)(a 2+2ab+b 2) = = a 3+2a 2b+ab 2 + a 2b+2ab 2+b 3 = = a 3+3a 2b+3ab 2+b 3 Так как равенство (1) верно при любых значениях a и b, то оно является тождеством. Это тождество называется формулой куба суммы. Если в эту формулу вместо a и b подставить какие-нибудь выражения, например 5y 3 и 2z, то опять получится тождество. (5y 3+2z) 3 = 125y 9+150y 6z +60y 3z 2+8z 3. (2) Поэтому формула куба суммы читается так: куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения и второго, плюс утроенное произведение первого выражения на квадрат второго, плюс куб второго выражения. |
| При любых значениях a и b верно равенство (a−b) 3 = a 3−3a 2b+3ab 2−b 3. (3) Доказательство. (a−b) 3 = (a−b)(a 2−2ab+b 2) = = a 3−2a 2b+ab 2 − a 2b+2ab 2−b 3 = = a 3−3a 2b+3ab 2−b 3 Так как равенство (3) верно при любых значениях a и b, то оно является тождеством. Эо тождество называется формулой куба разности. Если в эту формулу вместо a и b подставить какие-нибудь выражения, например 5y 3 и 2z, то опять получится тождество. (5y 3−2z) 3 = 125y 9−150y 6z +60y 3z 2−8z 3. (4) Поэтому формула куба разности читается так: куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения и второго, плюс утроенное произведение первого выражения и квадрата второго, минус куб второго выражения. |
30) Биномиальные коэффициенты.
В комбинаторике биномиальный коэффициент означает, число всех возможных вариантов выборки k элементов из множества элементов n.
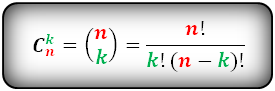
Пример:
Из множества n {1,2,3,4}, выбираем все возможные комбинации из двух элементов, k =2
{1,2} {1,3} {1,4} {2,3} {2,4} {3,4}
Получается шесть возможных вариантов.
Подставив значения в формулу, проверим полученный результат:
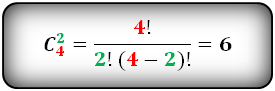
31,32,33)34,35
 2018-02-13
2018-02-13 904
904








