Квадратные уравнения. Правила

37) Для уравнений вида , то есть при чётном , где
вместо формулы (1) для нахождения корней можно использовать эквивалентное выражение

Действительно, подставим в вышеприведённую универсальную формулу (1) корней уравнения указанное соотношение:

Для приведённого квадратного уравнения эта формула принимает вид:

Также при чётном удобнее вычислять значение не целого дискриминанта, а его четверти:

или, если уравнение приведённое:

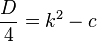Все необходимые свойства при этом сохраняются:

(вместо знака «больше» в выражение может быть подставлены и другие знаки: «меньше» или «равно»). Подобным преобразованиям можно подвергнуть формулу для нахождения единственного корня при :

Обратите внимание, что для приведённого уравнения можно упростить расчёт следующим образом:

Отсюда следует важное и полезное правило: корнем приведённого уравнения с чётным вторым коэффициентом и равным нулю дискриминантом является половина второго коэффициента.

38)