2018-02-13
835
Парная регрессия представляет собой регрессию между двумя переменными – 
и 
, т. е. модель вида:
,
где – зависимая переменная (результативный признак); – независимая, или объясняющая, переменная (признак-фактор). Знак «^» означает, что между переменными и нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина складывается из двух слагаемых:
,
где – фактическое значение результативного признака; 
– теоретическое значение результативного признака, найденное исходя из уравнения регрессии;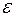 
– случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.
Случайная величина 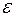называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения.
В парной регрессии выбор вида математической функции 
может быть осуществлен тремя методами:
1) графическим;
2) аналитическим, т.е. исходя из теории изучаемой взаимосвязи;
3) экспериментальным.
Спецификация парной линейной регр. модели имеет вид: Y=a+bX+ε, где a и b – параметры модели (постоянные неизвестные коэфф-ты), Х – экзогенная переменная (регрессор), У – эндогенная переменная (отклик), ε – случайное возмущение, характеризующее отклонение f(x)= a+bX (теоретической линей зависимости) и возникающее:
- из-за ошибок спецификации
- из-за ошибок измерений
Уравнения для отдельных наблюдений зависимой переменной У записываются в виде (схема Гаусса-Маркова)
Yt=a+bXt+εt, t=1,…,n – выборочные данные, n – объём выборки.
Относительно возмущений εt, в регр.моделях принимаются след. предположения (условия Гаусса-Маркова).
