2018-02-13
483
Класс функций, нелинейных по параметрам, в свою очередь, делится на два типа:
- нелинейные модели внутренне линейные;
- нелинейные модели внутренне нелинейные.
Внутренне линейные модели могут быть приведены к линейному виду.
Например.
1) 
- внутренне линейна, так как 
- линейна по параметрам;
2) 
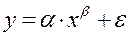- внутренне нелинейна;
3) 
- внутренне нелинейна;
4) 
- внутренне линейна, так как 
;
5) 
- внутренне линейна, так как 
;
5) 
- логистическая функция – внутренне линейна –
; 
; 
.
Замечание: чтобы получить аддитивный случайный член в уравнении регрессии, необходимо в исходной модели иметь мультипликативную случайную составляющую. Чтобы t- и F- критерии были применимы, необходимо, чтобы преобразованный случайный член имел нормальное распределение, т.е. исходный – логарифмически нормальное распределение
