2014-02-05
13437
Поверхности
Плоскость касательная к
 |
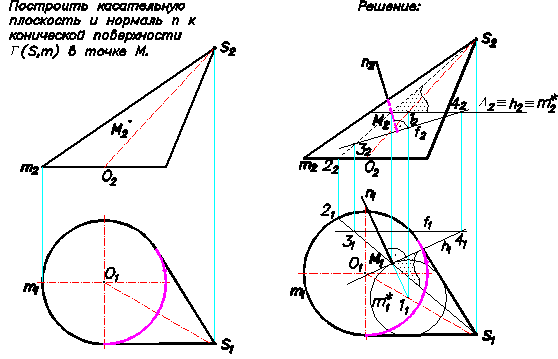Рис.61
Плоскость касательная к поверхности (П.К.П.) является геометрическим местом касательных прямых к линиям поверхности, проходящим через точку касания. Для задания такой плоскости достаточно построить касательные прямые к двум линиям, принадлежащим данной поверхности и проходящим через точку касания.
Пример 1. Построить плоскость S, касательную к конической поверхности Г (S,m) в точке М, принадлежащей данной поверхности. Построить нормаль n к конической поверхности Г в этой точке (Рис.61).
Плоскость, касательная линейчатой поверхности, включает в себя образующую этой поверхности, проходящую через точку касания. SM – образующая конической поверхности Г, проходящая через точку М.
При пересечении конической поверхности Г, проходящей через точку М горизонтальной плоскостью L(L 2 ) в сечении получим линию [окружность m*(m 1 *,m 2 *)], которая на горизонтальную плоскость проекций П1 спроецируется без искажения (m* 1 ). Приведенные на Рис.61 построения не представляют особого труда. Также построим на чертеже горизонталь h(h* 1 ,h* 2 ), касательную к окружности m* и проходящую через точку М. Плоскость S, сформированная двумя пересекающимися прямыми S(SM x h) и будет касательной плоскостью к конической поверхности Г в точке M.
Нормалью (перпендикуляром) к поверхности в определенной точке называется прямая, перпендикулярная к плоскости, касательной к данной поверхности в данной точке.
Построение перпендикуляра к плоскости было рассмотрено в лекции № 10 (2-я ОМЗ; перпендикулярность прямой и плоскости). В рассмотренном примере прямая n(n1,n2) является нормалью к поверхности Г в точке М.
[(n 1^ h 1; n 2^ f 2 ). Следовательно, n ^ S(SM x h) (f Ì S)].
Соответственно, прямая n является нормалью к поверхности Г в точке М.
Пример 2. Построить плоскость Г, касательную к поверхности вращения Φ в точке М(M 2 ). Построить нормаль n к поверхности вращения Φ в точке М(M 2 ).
 |
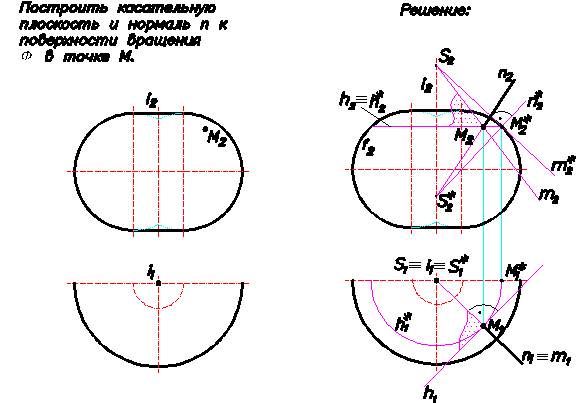Рис.62
Как уже указывалось выше, для построения плоскости, касательной к поверхности в какой-нибудь точке, достаточно построит проекции двух пересекающихся прямых, касательных к двум пересекающимся кривым, проходящих через точку касания. По аналогии с задачей, приведенной в примере 1, горизонталь h(h 1, h 2 ) является касательной к линии уровня h*(h* 1, h* 2 ) (окружности), проходящей через точку М(M 1, M 2 ). Выполненные построения очевидны из чертежа, приведенного на Рис.62. Принадлежащая линии уровня h*(h* 1, h* 2 ) точка М*(M* 1, M* 2 ) одновременно принадлежит и главному меридиану f(f 2 ) поверхности Φ. Напоминаю, что меридианами поверхности вращения называются линии, принадлежащие поверхности, и лежащие в плоскостях, проходящих через ось вращения поверхности. Меридиан f(f 2 ), расположенный в плоскости, параллельной фронтальной плоскости проекции П 2, называется главным меридианом. На плоскость П 2 Главный меридиан f(f 2 ) проецируется без искажения. Построим проекции прямой m*(m* 2 ), касательной к главному меридиану f(f 2 ) поверхности в точке M*(M* 2 ). Так как бразующая поверхности вращения Φ дуга окружности, выполнить такие построения не представляет особого труда. Касательная пересечет ось вращения i(i1, i2) в точке S(S1, S2) [касательная m*(m* 2 ) и ось i(i 1, i 2 ) обязательно пересекутся в точке S(S 1, S 2 ), так как обе прямые принадлежат плоскости главного меридиана f(f 2 )]. Точка пересечения S(S 1, S 2 ) является вершиной конуса вращения, касающегося поверхности врщения Φ по параллели h*(h* 1, h* 2 ). Прямая SM (образующая данного конуса) является касательной к поверхности Ф в точке М, как касательная к меридиану, проходящему через точку М. Две пересекающиеся прямые m(m 1, m 2 ) и h(h 1, h 2 ) сформируют плоскость Г(m x h), касающуюся поверхности вращения Ф в точке М.
Прямая n*(n* 2 ), перпендикулярная к фронтальной проекции m* 2 фронтали m* пересечет ось i(i 1, i 2 ) в точке S*(S* 1, S* 2 ). По аналогии с вышеприведенным конусом вращения, касающимся поверхности по параллели h*, точка S*(S* 1, S* 2 ) является вершиной конуса нормалей к поверхности вращения Ф в точках параллели h*. Прямая S*M (S* 1 M 1, S* 2 M 2 ) (образующая конуса нормалей) и является искомой нормалью n(n 1, n 2 ) к поверхности вращения Ф в точке М. Выполненные построения очевидны из чертежа, приведенного на Рис.62.
Лекция 14
Развертки поверхностей
Если отсек поверхностиможет быть совмещен с плоскостью без складок и разрывов, такая поверхность называется развертывающейсч, а полученная плоская фигура есть развертка данной поверхности.
Поверхности, которые не могут быть совмещенны с плоскостью, называются неразвертывающимися.
К группе развертывающихся поверхностеймогут быть отнесены только линейчатые поверхности. При этом только те из них, у которых касательная плоскость касается поверхности во всех точках прямолинейной образующей.
Основные свойства разверток поверхностей
1. Каждой точке (фигуре) на поверхности соответствует точка (фигура) на развертке и наоборот.
2. Длины соответствующих линий поверхности и ее развертки равны между собой.
3. Замкнутая линия на поверхности и соответствующая ей замкнутая линия на развертке ограничивают одинаковую площадь.
4. Угол между линиями на поверхности равен углу между соответствующими линиями на развертке.
5. Прямой на поверхности соответствует также прямая на развертке.
6. Параллельным прямым на поверхности соответствуют также параллельные прямые на развертке.
7. Если линии, принадлежащей поверхности и соединяющей две точки поверхности, соответствует прямая линия на развертке, то эта линия называется геодезической.
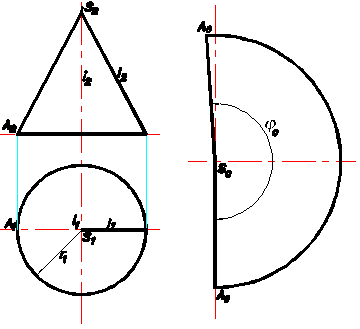
Пример 1 Построить развертку боковой поверхности прямого кругового конуса (Рис.63).
Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор, радиус S 0 A 0 которого равен образующей l конической поверхности, а центральный угол φ 0 определяется по формуле
φ 0= 360 х r: l,
где:
r - радиус основания конической поверхности;
l - образующая конической поверхности.
Рис.63
Пример 2 Построить развертку наклонной пирамидальной поверхности (Рис.63).
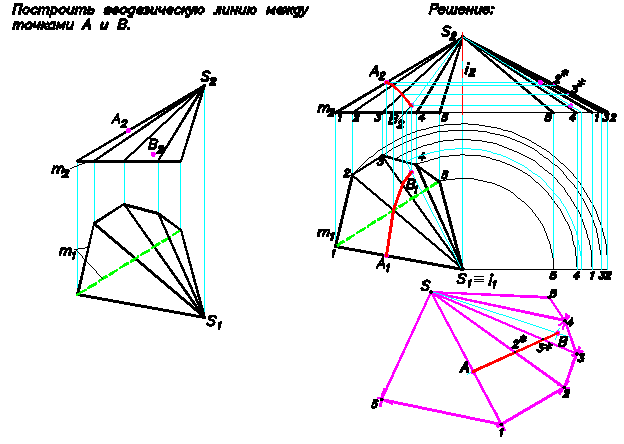
Рис.63
Для построения развертки боковой поверхности наклонной пирамиды (Рис.63)
определяются натуральные величины всех ребер пирамиды, а также сторон многоугольника основания. Натуральные величины боковых ребер наклонной пирамиды определены с помощью преобразования комплексного чертежа способом вращения вокруг горизонтально проецирующей оси i(i 1, i 2 ) (Лекция 12).Многоугольник основания m(m 1, m 2 ) пирамиды принадлежит горизонтальной плоскости уровня и поэтому на горизонтальную плоскость проекций П 1 все стороны многоугольника основания спроецировались в натуральную величину (m 1 - натуральная величина m). Определив натуральные величины боковых ребер и сторон основания наклонной пирамиды, построение развертки боковой поверхности пирамиды не представляет особого труда. Для построения развертки полной поверхности пирамиды необходимо к развертке боковой поверхности присоединить многоугольник основания пирамиды. Вышеописанные построения не представляют особой сложности и очевидны из чертежа, приведенного на Рис.63.
Пример 3 Построить развертку наклонной конической поверхности.
В таких случаях коническую поверхность заменяют поверхностью вписанной многоугольной пирамиды. Дальнейшие построения аналогичны приведенным в примере 2. Полученная развертка является приближенной разверткой наклонной конической поверхности. Чем большее число граней у вписанной пирамиды, тем меньше будет разница между действительной и приближенной развертками наклонной конической поверхностями.
Пример 3 Построить развертку призматической поверхности.
Если развертываемая призматическая поверхность задана на комплексном чертеже в общем виде (боковые ребра поверхности – прямые общего положения), предварительно комплексный чертеж призматической поверхности необходимо преобразовать до положения, когда боковые ребра станут линиями уровня. У приведенной на комплексном чертеже (Рис.64) трехгран-ной призматической поверхности боковые ребра - горизонтали. Далее мысленно «разрежем» призматичес-
кую поверхность вдоль ребра СС'. Используя теорию преобразования комплексного чертежа способом вращения вокруг линии уровня (Лекция 13), повернем грань СВВ'С' призмы вокруг ребра СС' (СС' - горизонталь и ось вращения) до положения плоскости уровня параллельной П 1).
Рис.64
. После этого последовательно повернем грань ВАА'В' призмы вокруг ребра ВВ' и грань АСС'А' вокруг ребра АА' до положения плоскостей уровня (параллельных П 1). Плоскости оснований призматической поверхности параллельны фронтальной плоскости проекций, поэтому прямые треугольников оснований на П 2 проецируются без искажения. Это обстоятельство значительно упрощает необходимые построения, выполненные на чертеже (Рис.64). Такой способ построения развертки называется Р А С К А Т К О Й. Для построения полной развертки поверхности призматической поверхности необходимо к развертке боковой поверхности присоединить треугольники оснований призмы.
Лекция 15
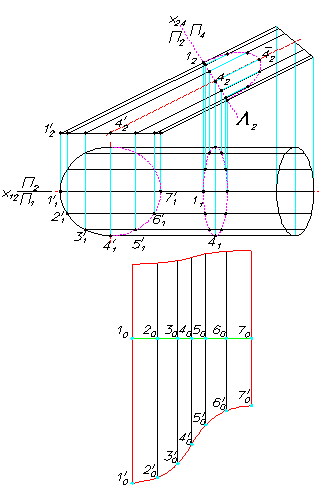Пример 4 Построить развертку наклонной цилиндрической поверхности (эллиптический цилиндр).
Для построения развертки цилиндри-
ческой поверхности используем способ нормального сечения (Рис.65). Так. как данная цилиндрическая поверхность имеет фронтальную плоскость симметрии, построим развертку ее половины.
Λ(Λ2) - фронтально проецирующая плоскость. Λ(Λ2) перпендикулярна
образующим цилиндра. Преобразуем комплексный чертеж способом перемены плоскотей проекций (вместо плоскости П1 введем плоскость П4). Такое преобразование позволит построить нормальное сечение цилиндрической поверхности без искажения.Отрезок 10 -70 на развертке равен длине половины линии нормального сечения. В обе стороны от данной ли-нии под прямым углом от определен-
ных точек отложены соответствующие отрезки образующих, действительные значения которых взяты с их фрон-тальной проекции. На приведенном комплекном чертеже (Рис.65) образу-ющие развертываемой цилиндричес-
кой поверхности – фронтали.
Рис.65
Пример 5. Построить развертку сферы.
При построении разверток поверхностей вращения часто применяют способ вспомогательных цилиндрических поверхностей. Поверхности вращения с помощью меридиан делят на равные части. На чертеже, приведенном на Рис.66, меридианами являются линии 1А (1 1, А 1 ) и 1В (1 1, В 1 ). Поверхность, заключенная между указанными меридианами, составляет одну двадцать четвертую часть поверхности сферы. Выделенный фрагмент поверхности сферы заменяют цилиндрической поверхностью, касающейся данного фрагмента сферы по среднему меридиану 1- 5 (1 1 - 5 1 ). Дальнейшие построения развертки фрагмента поверхности сферы понятны из чертежа, приведенного на Рис.66. Прямая 1 0 - 5 0 равна длине дуги 1 - 5. Ее проекция 1 2 - 5 2является натуральной величиной дуги 1-5, как фронтали. Отрезок А 0 В 0 равен длине отрезка АВ(А 1, В 1 ). И так далее. Полученная развертка поверхности сферы (одна двадцать четвертая ее часть) является приближенной.
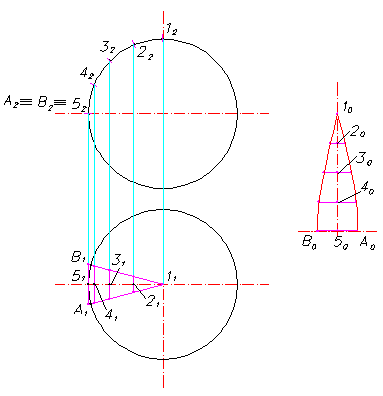
Рис.66
АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
При выполнении технических чертежей возникает необходимость иметь наглядный обратимый чертеж. Комплексный чертеж таковым не является. Таким является аксонометри-ческий чертеж.
Аксонометрический чертеж – это параллельная проекция на некоторую плоскость геометрического образа вместе с прямоугольной системой координат, к которой Г.О. относится.
 |
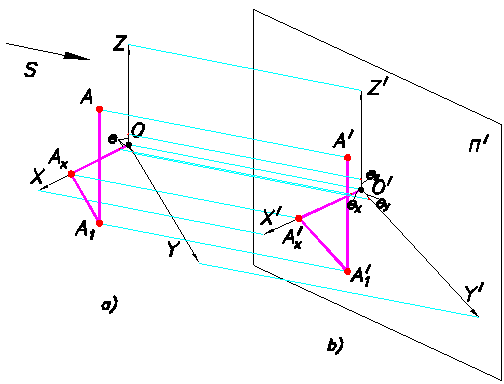Рис.67
Основные требования к чертежам.
| Комплексный чертеж | Аксонометри- ческий чертеж | |
| Быть простым в выполнении | + | - |
| Быть наглядным | - | + |
| Быть обратимым | + | + |
На Рис.67, a) приведен однокартинный чертеж точки А в натуральной (декартовой) системе координат.
· OXYZ - пространственная система прямоугольных координат;
· OX, OY, OZ - три взаимно перпендикулярные оси;
· XOY(П 1 ), XOZ(П 2 ), YOZ(П 3 ) - три взаимно перпендикулярные плоскости;
· А 1 - ортогональная проекция точки А на плоскость П 1;
· О А х А 1 А - координатная ломаная линия точки А в декартовой системе координат;
· е - единица длины (натуральный масштаб).
Отрезки координатной ломаной линии точки, измеренные единицей длины е, называются натуральными координатами точки А.
· О А х - абсцисса точки А или координата х точки А; х = ОА х: е;
· А х А 1 - ордината точки А или координата y точки А; y = А х A 1: е;
· А 1 А - аппликата точки А или координата z точки А; z = А 1 A: е.
А теперь рассмотрим Рис. 67, b). На плоскость П′ по направлению S спроецирована точка А вместе с декартовой системой координатных осей OXYZ, к которым она относится.
· А' - аксонометрическая проекция точки А;
· O'X′Y′Z′ - аксонометрическая система координат;
· О′ - начало аксонометрической системы координат;
· O′X′, O′Y′, O′Z′ - аксонометрические оси координат;
· О′ А′ х А′ 1 А′ - аксонометрическая координатная ломаная линия;
· A′ 1 - вторичная проекция точки А;
· О'А' х; А' х A' 1; А' 1 A' - аксонометрические координатные отрезки;
· е x, e y, e z - проекции натурального масштаба е на оси x, y и z соответственно и называются аксонометрическими масштабами;
· х' = О'А' х: е; y' = А' х A' 1: е; z' = А' 1 A': е - аксонометрические координаты точки А.
Если же измерить аксонометрические координатные отрезки соответствующими им аксонометрическими масштабами, получим натуральные координаты точки А.
О'А' х: е x = х; А' х A' 1: е y = y; А' 1 A': е z = z.
Для определения положения точки А на аксонометрическом чертеже недостаточно иметь только А' - её аксонометрическую проекцию. Ещё необходимо иметь А' 1 – вторичную проекцию точки А.
Показатели искажения
Показателями искажения по осям называются отношения аксонометрических координат точки А к её натуральным (декартовым) координатам (измеренным одной натуральной единицей е).
· u - показатель искажения по оси х; u = х': x = O'A' x: OA x = ex: e;
· v - показатель искажения по оси y; v = y': y = A' x A' 1: A x A 1 = ey: e;
· w - показатель искажения по оси z; w = z': z = A' 1 A': A 1 A = ez: e.
·
Лекция 16
Возникает вопрос, с какой степенью произвола могут быть заданы на аксонометрическом чертеже аксонометрические оси и аксонометрические масштабы?
Ответ. Всегда в пространстве найдется такое положение прямоугольной системы натуральных координат и такое направление проецирования, что любая аксонометрическая система окажется параллельной проекцией натуральной системы (Теорема Польке).
Показатели искажения u, v и w и угол φ образованный направлением проецирования с плоскостью проекций, связаны соотношением
u 2 + v 2 + w 2 = 2 + ctg2 φ.
Это соотношение легко доказывается в частном случае, когда две из координатных оcей парал-лельны (или совпадают) аксоно-метрической плоскости проек-ций. Пусть, к примеру, плоскость xОy совпадет с плоскостью П ′ (см. Рис.68). xOy ≡ П′
(О ≡ О′; x ≡ x′; y ≡ y′).
Из чертежа (Рис.68) видно, что
u = e' x: e =1;
v = e' y: e =1;
w = e' z: e = ctg φ (направление проецирования S под углом φ к аксонометрической плоскости проекций П.Из полу-ченных результатов (последние три формулы) следует вышепри-веденное соотношение
Рис.68 u 2 + v 2 + w 2 = 2 + ctg2 φ.
Оно справедливо и в общем виде (мы рассмотрели частный случай). При ортогональ-ной аксонометрии (φ = 90 о; следовательно, ctg φ = 0) получаем, что
u 2 + v 2 + w 2 = 2.
Виды аксонометрий
1. В зависимости от направления проецирования;
· - косоугольная аксонометрия (φ ≠ 90 о);
· - прямоугольная (ортогональная) аксонометрия (φ = 90 о).
2. В ортогональной аксонометрии в зависимости от соотношения между показателями искажения координат:
· u = v = w - ортогональная изометрия;
· u = v ≠ w; u = w ≠ v; v = w ≠ u - ортогональные диметрии;
· u ≠ v ≠ w - триметрия.
