Описание эксперимента

В настоящей работе предлагается на частном примере убе­диться, что распределение интенсивности света в фокальной плоскости линзы представляет собой квадрат фурье-образа рас­пределения амплитуды во входной плоскости линзы.

Поместим во входной плоскости линзы узкую щель, ширина которой равна , а длина   а, как показано на рис. 2. На щель направим плоскую световую волну с волновым векто­ром, параллельным оптической оси. Амплитуду волны обозначим .Тогда в плоскости расположения щели для точек внутри щели , а для точек вне щели = 0. Распределение амплитуды света в фокальной плоскости линзы будет иметь вид:

                     (9)

 

Поскольку интенсивность света пропорциональна квадрату ам­пли-туды, для распределения интенсивности в фокальной плос­кости имеем:

,                    (10)

где  – интенсивность света в точке с координатами х = 0, у = 0.

Два сомножителя в выражении (10) имеют вид функции . График этой функции показан на рис. 3.

Рис. 3

 

Минимум этой функции наблюдается при

,  = ±1, ±2,...                        (11)

Из выражений (10) и (11) следует, что ширина центрального мак­симума вдоль оси х,т.е. расстояние между –1 и +1 минимумами, равно

f / b,

а вдоль оси у –

f / b.

В нашей установке длина щели 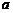 во много раз больше ширины щели . Поэтому . Это означа­ет, что свет в фокальной плоскости линзы сосредоточен в виде узкой полоски, вытянутой вдоль оси х при у = 0. Зависимость интенсивности света от координаты х в этой полоске определя­ется формулой

                             (12)

и преобразование Фурье можно считать одномерным.

Для того чтобы убедиться экспериментально, что распределе­ние интенсивности света в фокальной плоскости линзы соответ­ствует формуле (12) и тем самым подтвердить, что это распре­деление пропорционально квадрату фурье-образа функции 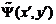, можно определить координаты для некоторых мини­мумов и максимумов функции  и величину  для не­которых максимумов и сравнить эти данные с рассчитанными теоретически в соответствии с формулой (12).

Исследовав функцию  на экстремум, можно заключить, что минимумы будут наблюдаться в точках с координатами

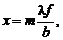
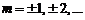                                  (13)

Центральный максимум наблюдается при х = 0. Максимумы более высоких порядков расположены не точно посредине между минимумами. Ниже приведены выражения для координат максимумов ±1,±2 и ±3 порядков:

	x ±1 = ±1,430l f / b» ±1,5l f / b, x ±1 = ±1,430l f / b» ±1,5l f / b, x ±1 = ±1,430l f / b» ±1,5l f / b.

 

(14)

                                

 

Значения функции   в центральном и трех последующих максимумах соотносятся как

	1:0,047:0,017:0,0083.

                (15)

 

Расстояние между соседними максимумами (или минимума­ми) в фокальной плоскости линзы невелико. Поэтому для удобст­ва измерений с помощью другой линзы в некоторой плоскости создается действительное увеличенное изображение картины распределения света в фокальной плоскости. В этой плоскости располагается фотоприемник. Если в плоскости фотоприемника ось X направить параллельно оси х, а начало отсчета совмес­тить с положением центрального максимума, то изображение точки, имеющей в фокальной плоскости координату х, будет иметь в плоскости фотоприемника координату X, причем , где  – коэффициент увеличения.

Измерив координаты максимумов и минимумов в плоскости фотоприемника, можно вычислить соответствующие координаты в фокальной плоскости линзы по формуле

.                                         (16)