Закон сохранения массы и уравнения неразрывности

Закон сохранения массы для изолированной системы выражается в том, что масса m такой системы остается постоянной во время движения. Следовательно, полная производная от массы по времени равно 0.

 

Используя закон сохранения массы для элементарного объема получим:

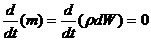
После дифференцирования будем иметь

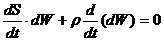
Второе слагаемое деленное на ρdW есть величина относительного изменения объема dW, равная

сумма диагональных компонент тендора скоростей дифференциальный

/Тогда получим

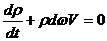Уравнение неразрывности, является выражением закона сохранения массы.

Если жидкость несжимаема,то есть ρ=const, то уравнение неразрывности примет вид:

 

 

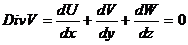
2, Закон сохранения количества движения (импульса). Дифференциальные уравнения динамики жидкости в напряжениях.

Закон сохранения импульса можно сформулировать так:

«Разность векторной производственной от количеств движения жидкого объема и всех внешних сил, приложенных к нему, равна нулю во все время движения».

 

 

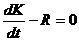
 Для конечного объема жидкости W с поверхности S закон сохранения импульса   можно записать

 

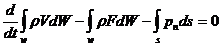
 Путем математических преобразований получаем закон сохранения импульса в векторной форме:

, где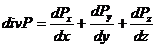

 Закон сохранения импульса в проекциях на оси координат можно записать:

 

 

 

 

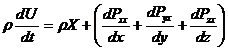
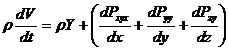
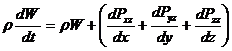
Лекция 5