1) Из определения углового ускорения 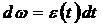 находится угловая скорость как функция времени:
находится угловая скорость как функция времени: 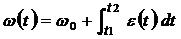 . (w 0 – константа интегрирования).
. (w 0 – константа интегрирования).
2) Из определения угловой скорости 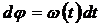 находится угол как функция времени:
находится угол как функция времени: 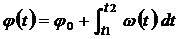 . (j 0 – константа интегрирования).
. (j 0 – константа интегрирования).
Для частного случая 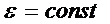 , получаем закон равнопеременного движения по окружности:
, получаем закон равнопеременного движения по окружности: 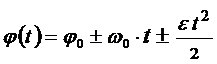 – квадратичная зависимость угла поворота от времени
– квадратичная зависимость угла поворота от времени
и линейная зависимость угловой скорости от времени 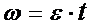 .
.
При этом одинаковым знакам для угловых скорости и ускорения 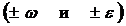 соответствует ускоренное движение, а разным знакам
соответствует ускоренное движение, а разным знакам 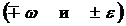 – замедленное.
– замедленное.
Динамика вращательного движения
Работа при вращательном движении. Момент силы
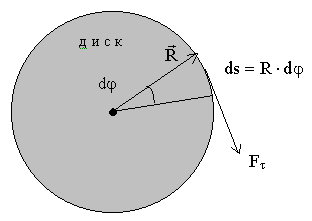
Элементарная работа на пути ds=Rdj равна 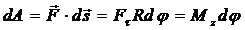 , где момент силы относительно оси вращения z (вращающий момент)
, где момент силы относительно оси вращения z (вращающий момент)
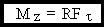 .
.
В векторном виде:
Кинетическая энергия при вращательном движении. Момент инерции
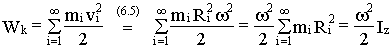 .
.
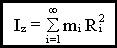 .
.
Iz - момент инерции твердого тела, относительно оси z.
Моментом инерции материальной точки Ii называется величина:
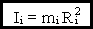 .
.
Для N материальных точек 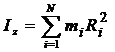
Для сплошного тела 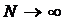 и для вычисления момента инерции твердого тела необходимо брать интегрирал
и для вычисления момента инерции твердого тела необходимо брать интегрирал 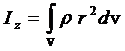 (учтено, что dm=rd v).
(учтено, что dm=rd v).
Величина I зависит от положения оси вращения и от распределения масс в теле.
Теорема Штейнера
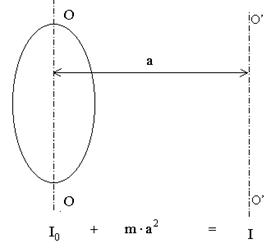
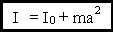 ,
,
где I0 - момент инерции относительно оси OО,
I - момент инерции относительно оси O'О'.
Моменты инерции I0 для некоторых тел (относительно оси, проходящей через центр масс).
Для сплошного тела момент инерции 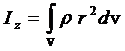
1. Обруч массой m и радиусом R с однородным распределением массы:
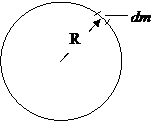 r d v = dm
r d v = dm
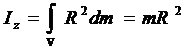
2. Полый цилиндр – состоит из одинаковых обручей: 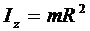
3. Сплошной цилиндр. Выделим элемент площади ds = 2p rdr,
 элемент объёма d v = hds=2p rhdr.
элемент объёма d v = hds=2p rhdr.
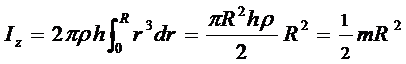
4. Тонкий однородный стержень длиной L.
1) Ось проходит через середину стержня.
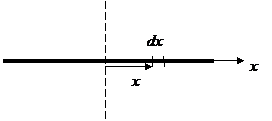 элемент массы dm = rdx (r – линейная плотность массы).
элемент массы dm = rdx (r – линейная плотность массы).
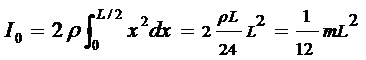
2) Ось проходит через конец стержня.
По теореме Штейнера 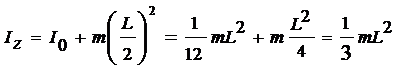
5. 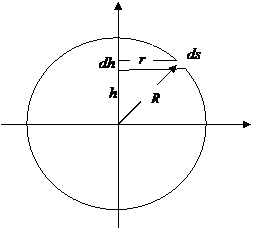 Шар. Разобьем шар на плоские цилиндры (блины) шириной dh: объём,
Шар. Разобьем шар на плоские цилиндры (блины) шириной dh: объём,
радиус и масса этого элементарного цилиндра
d v = p r 2 dh, r 2 = R 2 - h 2 , 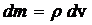 .
.
Момент инерции этого элементарного цилиндра 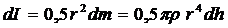 .
.
Интегрируя по h от 0 до R и удваивая, получим
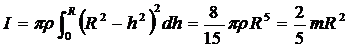
6. Шаровой слой. Внутренний и наружный радиусы: R 1 и R 2.
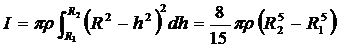
7. Сферическая оболочка.
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
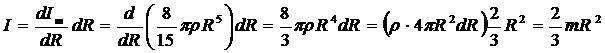
 2018-02-13
2018-02-13 1033
1033

 -
-