Інтегрування функції комплексної змінної

 

Обчислення інтеграла від функції комплексної змінної зводится до обчислення звичайних криволінійних інтегралів. Якщ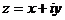о , , то .

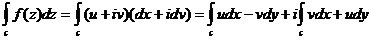.(як я зрозумів цю формулу)

Теорема Коші. Якщо функція  аналітична в обов’язковій області, обмеженій замкненим контуром Г, а також в точках цього контура, то

    Г

У випадку багатов’язної(!!!!) області

;

У випадку двов’язної області (Мал. 10)

 (не зрозумів, що за буква під другим інтегралом(поставив ГАММУ))

Г

    Мал. 10

 

Інтегральна формула Коші.

Розглянемо інтеграл , де Г -замкнений контур, обмежуючий область D. Якщо точка 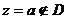, то  аналітична функція всередині D і на Г. Тоді на підставі теореми Коші:

   

 

Нехай точка  і обходиться контуром Г в додатному напрямі 1 раз. Вибравши коло (та ж проблема) радіусом R з центром в точці а, тобто

, , знайдемо .

Отже, .

 

Теорема. Якщо функція  аналітична в області D, обмеженій замкненим контуром Г, і на самому контурі Г, то

    , (1)

де , , і контур Г обходиться в додатному напрямі. Рівність (1) називається 1-ою інтегральною формулою Коші, а інтеграл  -

інтегралом Коші.

 

Інтеграли типу Коші.

Теорема. Якщо функція  аналітична в області D і на її границі Г, то для довільного натурального n можна записати формулу

    , (2)

де , .

Рівність (2) називається 2-ою інтегральною формулою Коші, а інтеграл

- інтегралом типу Коші.

 

Приклади.

1. Обчислити 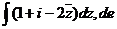(2z-незрозуміло!)

    а) с-відрізок   б) с-дуга параболи , ;

    в) с-відрізки  V , ( ).

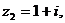
Рішення:

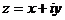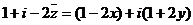Якщо , , то , де , .

За формулою

маємо:

.

1+i-2

Мал. 11

а) Контур С-відрізок 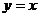,  (Мал. 11)

тому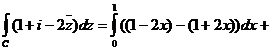

 

0 Z1

Z2

Мал. 12

б) Контур С-дуга параболи ;

(Мал. 12)

маємо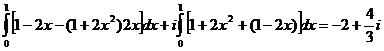

(скобка до «і» в методичці стоїть)

---

---