Числа (потрібен чи не потрібен абзац?) виду 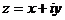 , де
, де 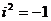 , називаються комплексними.
, називаються комплексними.
 - дійсна частина комплексного числа;
- дійсна частина комплексного числа;
 - уявна частина комплексного числа;
- уявна частина комплексного числа;
Комплексне число 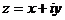 в деякій Декартові системі координат зображується точкою
в деякій Декартові системі координат зображується точкою  з координатами
з координатами  або радіус-вектором точки (мал.1). Із геометричного змісту комплексного числа (мал.1) зрозуміло, що
або радіус-вектором точки (мал.1). Із геометричного змісту комплексного числа (мал.1) зрозуміло, що 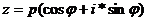 (1) або
(1) або  (2)
(2)
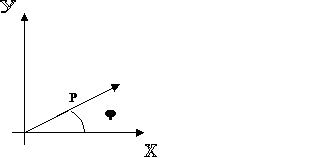
Мал.1
(1)- тригонометрична форма комплексного числа
(2)- експоненціальна форма комплексного числа

 - модуль комплексного числа, а
- модуль комплексного числа, а 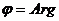
 - аргумент, де
- аргумент, де 

 (
(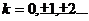 );
);  -головний кут і
-головний кут і  ;
;  (
(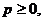

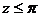 ).
).  називається комплексно-спряженим числом.
називається комплексно-спряженим числом.
Дії над комплексними числами:
Нехай  і
і  , тоді:
, тоді:
1.  , якщо
, якщо  і
і  (
(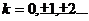 )
)
2.  (!)
(!)
3.  (!)
(!)
4. 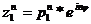 , має місце формула Муавра: (!)
, має місце формула Муавра: (!)  ;
;  (по поводу чего в методичке написано????)
(по поводу чего в методичке написано????)
5.  , або
, або 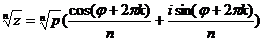 , k=0,1,2,…, (n-1).
, k=0,1,2,…, (n-1).
Приклади: виконати указані дії, якщо (z=2+5i):
1) 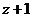 2)
2)  3)
3)  4)
4) 
5)  6)
6)  (В методичке другое) 7)
(В методичке другое) 7)  8)
8) 
9) 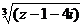 10)
10)  11)
11) 
Розв’язки
1) 
Радіус-вектор 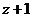 дорівнює сумі двох радіус-векторів
дорівнює сумі двох радіус-векторів  та
та  (мал. 2).
(мал. 2).






Мал. 2
2) 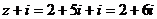
Радіус-вектор 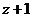 дорівнює сумі радіус-векторів
дорівнює сумі радіус-векторів  та
та  (мал. 3).
(мал. 3).

Мал. 3
3) 
Радіус-вектор  дорівнює сумі радіус-векторів
дорівнює сумі радіус-векторів  та
та 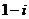 (мал. 4).
(мал. 4).

Мал. 4
4)  ;
;  або за формулою Мавра
або за формулою Мавра 
 (була помилка)
(була помилка)
 ; k є Z.
; k є Z.
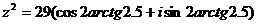

5) 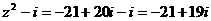
6) 
 (не зрозуміла помилка)
(не зрозуміла помилка)
7)  або
або 
Маємо:
 ;
;  =
= 
Або:

8)  ;
;
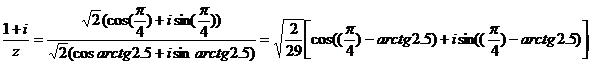

9) 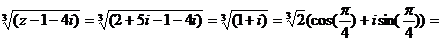 (в останньому не зрозуміло, під корнем весь вираз чи тільки «2-ійка»)
(в останньому не зрозуміло, під корнем весь вираз чи тільки «2-ійка»)
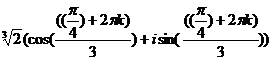 , k=0,1,2
, k=0,1,2

10)  , k=0,1
, k=0,1

11)  k=0,1
k=0,1
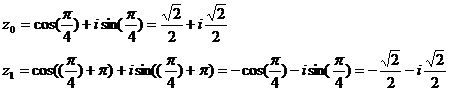
Приклади
В площині  зобразити геометричні місця точок для заданих співвідношень:
зобразити геометричні місця точок для заданих співвідношень:
1)  ;
;  ;
; 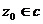 ;
; 
2)  ;
;  ,
, 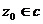 ,
, 
3)  ;
;  ,
,  ;
; 
4) 
5)  ,
, 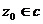 ,
, 
Розв’язки:
1)  . Маємо:
. Маємо:  ,
, 
Тоді  ,
,  (В методичці на початку рів-ня опечатка, або так потрібно(порядковий номер “Y”… і в ньому стоїть знак додавання))
(В методичці на початку рів-ня опечатка, або так потрібно(порядковий номер “Y”… і в ньому стоїть знак додавання))
Звідси випливає, що 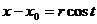 ,
,  ,
,  - параметричні рівняння кола радіуса
- параметричні рівняння кола радіуса 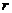 з центром в точці (
з центром в точці ( ), (мал. 5)
), (мал. 5)

Мал. 5
Маємо 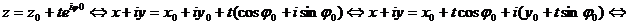
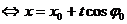 ;
;  , (<=Повторюється...!)
, (<=Повторюється...!)
 - параметричні рівняння прямої
- параметричні рівняння прямої 
Включаючи параметр  , маємо:т
, маємо:т  ,
,  (мал. 6)
(мал. 6)

Мал. 6 Мал. 7
3) З  ,
,  , випливає, що вектори
, випливає, що вектори  та
та  колінеарні.
колінеарні.
Геометричне місце точок  є пряма, що проходить через точки
є пряма, що проходить через точки 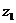 і
і  (мал. 7)
(мал. 7)
4) Модуль різниці двох комплексних чисел  в площині
в площині  дорівнює відстані між точками
дорівнює відстані між точками  і
і 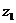 , тому
, тому 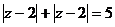 є сума відстаней довільної точки
є сума відстаней довільної точки  від двох точок
від двох точок  і
і  і дорівнює 5. Отже, геометричне місце точок
і дорівнює 5. Отже, геометричне місце точок  є еліпс з фокусами в точках
є еліпс з фокусами в точках 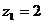 і
і  , велика вісь еліпса дорівнює 5 (мал. 5)
, велика вісь еліпса дорівнює 5 (мал. 5)
5) Оскільки  дорівнює відстані між точками
дорівнює відстані між точками  і
і  то
то 

 є геометричне місце точок
є геометричне місце точок  , відстань яких до даної точки
, відстань яких до даної точки  менше за
менше за 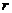 , тобто коло радіуса
, тобто коло радіуса  є центром в точці
є центром в точці  (мал. 9).
(мал. 9).

(в методичці є незрозумілості в обох малюнках) Мал. 8 Мал. 9
 2018-02-13
2018-02-13 516
516







