Для того, щоб функція 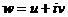 була диференційована в точці
була диференційована в точці 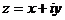 необхідно і достатньо, щоб виконувались умови Коші-Рімана:
необхідно і достатньо, щоб виконувались умови Коші-Рімана:
 і
і 
Похідна функції комплексної змінної знаходиться за формулами:
 .
.
Геометричний зміст похідної функції комплексної змінної:
1. Модуль похідної  виражає розтяг або стискання відстані між образами точок
виражає розтяг або стискання відстані між образами точок  і
і  при відображенні
при відображенні  площини
площини  на площину
на площину  .
.
2. Аргумент похідної  характеризує кут
характеризує кут  , на який треба повернути дотичну в точці
, на який треба повернути дотичну в точці  кривої площини
кривої площини  , щоб отримати напрямок дотичної в точці
, щоб отримати напрямок дотичної в точці 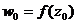 до образу цієї кривої на площині
до образу цієї кривої на площині  при відображенні
при відображенні  .
.
Приклади:
1) Довести, що функція  диференційована у всіх точках площини і знайти її похідну.
диференційована у всіх точках площини і знайти її похідну.
Розв’язок:
Маємо  ,
, 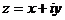 . Тоді
. Тоді  . Тому
. Тому  ,
,  . Знаходимо
. Знаходимо  ,
,  ,
,  ,
,  .
.
Окільки ця функція задовольняє умовам Коші-Рімана  ,
,  , то вона диференційована. Її похідну знаходимо за формулою
, то вона диференційована. Її похідну знаходимо за формулою  .
.
Маємо:  .(не впевнений в вірності степені «x+iy»а не «x+yi»...). Отже
.(не впевнений в вірності степені «x+iy»а не «x+yi»...). Отже  .
.
2) Знайти коефіцієнт розтягу  , та кут повороту
, та кут повороту  в точці
в точці  при відображенні функцією
при відображенні функцією  .
.
Розв’язок:
 , якщо
, якщо  ,
,  .(В методичці К россійська!). Знаходимо
.(В методичці К россійська!). Знаходимо  , отже
, отже  .(!!!....!!!-не зрозуміла нісенітниця в записах методички). Маємо:
.(!!!....!!!-не зрозуміла нісенітниця в записах методички). Маємо:  ;
;  ;(здається не вірно).
;(здається не вірно).
3) Маємо уявну частину  (перепровірити) диференційної функції
(перепровірити) диференційної функції  . Знайти цю функцію.
. Знайти цю функцію.
Розв’язок:
Маємо  . Тоді
. Тоді  . Скориставшись формулою Коші-Рімана
. Скориставшись формулою Коші-Рімана  , маємо
, маємо  . Звідси
. Звідси 
 . Отже,
. Отже,  , скориставшись другою умовою Коші-Рімана
, скориставшись другою умовою Коші-Рімана  , маємо
, маємо  . Отже,
. Отже,  , або
, або  . Звідси маємо
. Звідси маємо 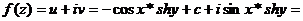
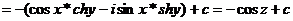 .
.
 2018-02-13
2018-02-13 921
921








