Моментные функции случайных процессов

1. Математическое ожидание случайного сигнала (по сечению)

Непрерывный сигнал:

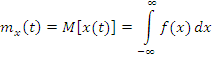
Дискретный по амплитуде (квантованный) сигнал:

2. Начальные моменты k -го порядка:

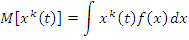
3. Центральные моменты k -го порядка:

4. Центральный момент 2-го порядка – дисперсия:

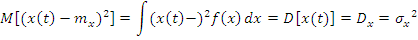
Для описания/моделирования временной взаимосвязи сечений случайного процесса используется:

  корреляционная функция:

Ковариационная функция

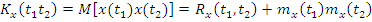
При

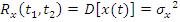
Нормирование корреляционной и ковариационной функции:

Свойства:

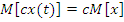
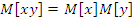
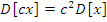
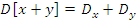
Допущения и упрощения при моделировании случайных процессов:

Стационарность:

· В широком смысле:  и  – и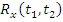нвариантны относительно сдвига во времени:

 

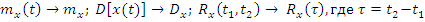
· В узком смысле:  - инвариантны относительно сдвига во времени.

Эргодичность:

Моментные функции, полученные для сечений с вероятностью, стремящейся к 1, совпадают со средними значениями, полученными на оной реализации по времени наблюдения

Для характеристики стационарных в широком смысле случайных процессов в частотной области используется 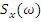 – спектральная плотность стационарного случайного процесса – преобразования Ф от корреляционной функции (в комплексной форме):

Физический смысл - разложение средней мощности случайного сигнала по частотам.

Действительная форма спектрального разложения:

При этом  при

Свойства корреляционных функций

Для стационарных процессов:

1) 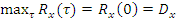 или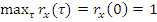

2)

 

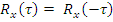
Для эргодических процессов:

3)

Эффективный интервал корреляции

1.

2.

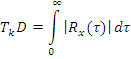
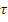
3. – неслучайная функция,

то   не изменится.

т.к. 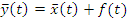, то

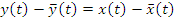 и т.д.

4. - неслучайная функция,

то

5.