Периодический сигнал
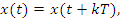
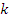 – целое,
– целое,
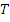 – период.
– период.
Пример:
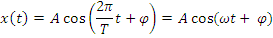
Любой спокойный периодический сигнал может быть представлен в виде композиции гармонических колебаний с частотами, кратными основной частоте.
ω = 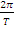
f= 
Примеры
К периодическим сигналам относят:
· Гармонические:
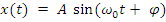
· Полигармонические:
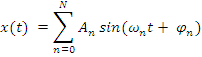
Полигармонические сигналы могут включать постоянную составляющую 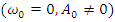 и сумму гармонических с любыми значениями амплитуд гармоник и фаз с частотами, кратными фундаментальной частоте
и сумму гармонических с любыми значениями амплитуд гармоник и фаз с частотами, кратными фундаментальной частоте 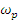 , равной или кратной минимальной частоте гармоник.
, равной или кратной минимальной частоте гармоник.
Непериодические сигналы
Понятие интервала наблюдения 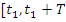 ],
],
Вставка: преимущества гармонического (sin/cos) разложения периодических сигналов.
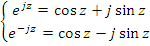
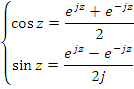
Информационные параметры детерминированных сигналов
Интервал наблюдения не должен быть меньше (для периодического сигнала) периода основной гармоники:
· Максимальное (пиковое) значение на 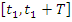
· Постоянная составляющая (среднее значение):
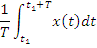
· Средневыпрямленное значение:
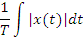
· Среднеквадратичное значение (действующее):
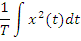
С энергетических позиций - сигналы с бесконечной и конечной (ограниченной) энергией:
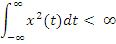
· Апериодические сигналы без постоянной составляющей.
· Импульсные сигналы.
Случайные сигналы
Случайным сигналом называют временную функцию, значения которой априори на интервале наблюдения не известны. Случайный сигнал содержит две компоненты:
· Полезный сигнал
· Шум (помеха)
Источники помех/шумов:
· Внутренние (тепловые шумы)
· Внешние:
§ Индустриальные
§ Флуктуации внешней среды
§ Молнии
§ Специальные наводки
Классификация по временным/ частотным свойствам:
· Флуктуационные
· Импульсные
· Периодические
Основные модели взаимодействия полезного сигнала и шума:
· Аддитивные 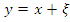
· Мультипликативные 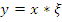
· Комбинированные 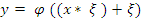
Типы сигналов:
1. Аналоговый сигнал:
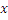
|
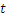
|
2. Дискретный сигнал - последовательность отсчетов:
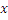
|
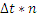
|
3. Квантованный сигнал (по амплитуде):
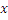
|
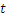
|
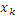
|
4. Цифровой сигнал – дискретный + квантованный
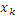
|
|
Преобразования типа сигнала:
· Дискретизация
· Квантование
· Аналогово-цифровое (АЦП)
· Восстановление (например, ЦАП)
Формы представления математических моделей сигналов:
· Во временной области (аргумент время)
· В частотной области (аргумент частота)
Представление в частотной области – спектральное.
Спектры детерминированных сигналов
a) Спектры гармонических сигналов
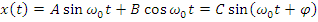
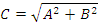
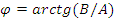
Спектр сигнала содержит общую составляющую 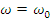 с амплитудой, равной
с амплитудой, равной 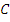 .
.
b) Спектры периодических сигналов произвольной формы:
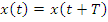
Спектр может бытьполучен (представляем сумму гармонических сигналов) путем разложения в гармонический ряд Ф.
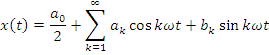
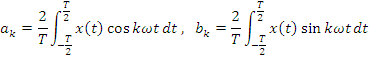
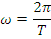
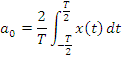
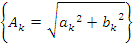 – амплитудный спектр;
– амплитудный спектр;
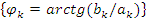 – фазовый спектр;
– фазовый спектр;
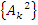 – энергетический спектр.
– энергетический спектр.
c) Спектры непериодических сигналов
Методически 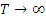 .
.
Спектральное разложение детерминированного непериодического сигнала называется преобразованием Ф.
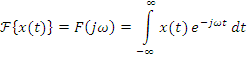
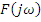 – комплексный амплитудный частотный спектр
– комплексный амплитудный частотный спектр
| 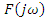 |- амплитудный спектр
|- амплитудный спектр
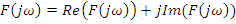
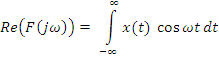
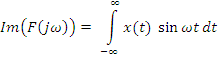
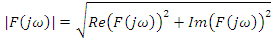
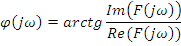
Свойства преобразования Ф.
1. 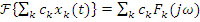
2. 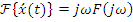
3. 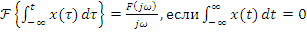
4. 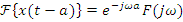
5. 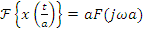
6. Теорема Парсеваля
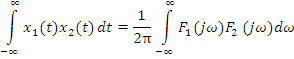
Для математического моделирования операций преобразования типов сигналов используют специальные пробные функции:
1. δ - функция Дирака:
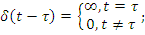
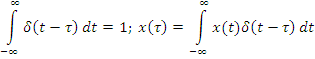
| δ |
| τ |
| t |
2. функция Кронекера (аналог δ функции для дискретных сигналов):
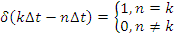
| δ |
k 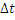
|
| 1 |
n 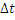
|
3. Единичная функция Хевисайда: для создания математических моделей сигналов конечной длительности.
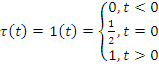 (или 1,
(или 1, 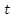 =0)
=0)
Тема 2. Вероятностные методы теории информационных процессов.
Случайные события
Любой принятый сигнал апостериорно представляет собой детерминированный процесс или событие. Априорно наблюдатель/приемник не знает в точности поведение сигнала, он для него не определен, т.е. случаен.
Математический аппарат описания априорно неопределенных процессов или событий:
· Теория вероятности
· Теория нечетных множеств
Теория вероятностей:
· Статистический подход
· Аксиоматический подход (Колмогоров)
Объекты теории вероятности:
· случайные события
· случайные величины
· случайные вектора
· случайные процессы
Случайное событие – произошло или нет, мера случайности – вероятность 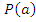 .
.
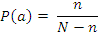
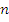 - да
- да
N – всего событий, 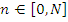
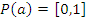
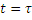
|
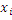
|
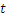
|
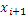
|
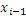
|
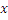
|
Событие: 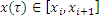
|
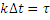
|
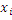
|
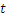
|
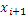
|
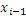
|
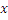
|
Событие: 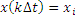
|
Случайная величина 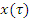
| τ |
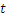
|
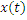 - принятый сигнал - принятый сигнал
|
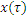 - сечение - сечение
|
| Одна реализация |
| T=τ |
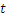
|
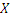
|
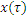 - сечение - сечение
|
| Ансамбль реализаций |
Случайный вектор 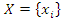 , где
, где 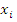 - случайная величина.
- случайная величина.
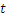
|
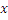
|
 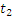 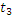 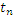


|
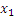 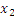 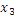 


|
Другой пример случайных событий – сигналы систем контроля состояния (логические сигналы). ИИС может одновременно фиксировать несколько случайных событий, т.е. ансамбль событий, например, смотрите рисунок выше.
А: 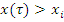
B: 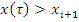
С: 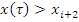
Эти события могут быть зависимыми или независимыми.
Отношения событий
Сумма: 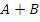 – по крайней мере одно событие имеет место.
– по крайней мере одно событие имеет место.
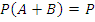
Формула сложения вероятности:
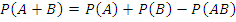
Произведение: 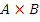 – и то, и это событие одновременно.
– и то, и это событие одновременно.
Формула умножения вероятности:
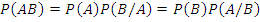
Здесь 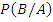 - условная вероятность.
- условная вероятность.
Несовместимые события:
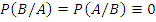
Несовместимые события образуют полную группу, если ∑ вероятности этих событий = 1. Обычно 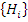 - ансамбль гипотез,
- ансамбль гипотез, 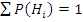
Формула полной вероятности
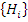 - ансамбль гипотез (полный).
- ансамбль гипотез (полный).
Событие 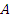 может произойти только совместно с одной из гипотез.
может произойти только совместно с одной из гипотез.
Очевидно, 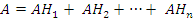
Тогда 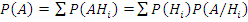
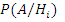 - апостериорная условная вероятность.
- апостериорная условная вероятность.
Пусть 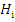 – вероятность состояния сигнала (сообщения), и нас интересуют априорные условные вероятности посылки s w:val="24"/></w:rPr><m:t>H</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>i</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
– вероятность состояния сигнала (сообщения), и нас интересуют априорные условные вероятности посылки s w:val="24"/></w:rPr><m:t>H</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>i</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 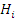 , если мы получили
, если мы получили 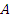 .
.
Тогда формула Байеса:
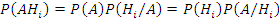
Но 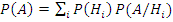 , следовательно:
, следовательно:
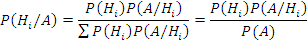
Случайный процесс как модель сигнала
В общем случае определяемая одномерной или многомерной функцией распределения и плотностью распределения вероятности.
Одномерная модель (модель сечения сигнала в момент t=t0)
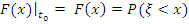
ξ - фиксируемая случайная величина или 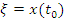
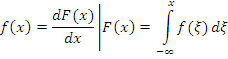
Многомерная модель (случайный процесс – статистический ансамбль выборочных функций)
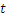
|
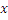
|
 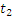 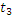 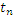


|
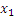 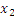 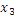 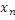


|
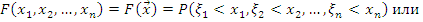
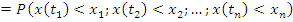
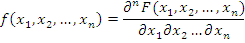
Здесь 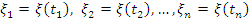
Чаще всего ограничиваются исследованием одномерных и двумерных моделей.
Свойства функций и плотности распределения вероятности.
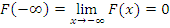
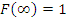 Если
Если 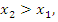 то то 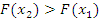 ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 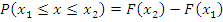
| 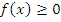
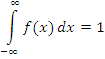
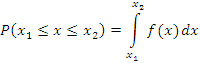
|
Для дискретных по величине случайных сигналов (квантованных):
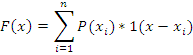
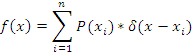
 2018-02-14
2018-02-14 174
174







