Понятие простейшей случайной функции:

 – детерминированная функция
– детерминированная функция
 – случайная величина.
– случайная величина.
Тогда 
Если  , то
, то 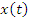 – элементарная случайная функция. Для нее
– элементарная случайная функция. Для нее

Любую центрированную случайную функцию  можно представить в виде взаимно некоррелируемых случайных элементарных функций
можно представить в виде взаимно некоррелируемых случайных элементарных функций

Из взаимной некорр.  следует некоррелируемость s w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>i</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
следует некоррелируемость s w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>i</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  .
.


В силу взаимной некорр.  остается один член при
остается один член при  , равный s w:val="24"/></w:rPr><m:t>D</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/><w:lang w:val="EN-US"/></w:rPr><m:t>i</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
, равный s w:val="24"/></w:rPr><m:t>D</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/><w:lang w:val="EN-US"/></w:rPr><m:t>i</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 

Произвольная нецентрир. случайная функция:

Это и есть каноническое разложение.
s w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>i</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  - коэффициент разложения,
- коэффициент разложения,
 - координатные функции.
- координатные функции.
При 

Таким образом, зная каноническое разложение  , можно сразу получить каноническое разложение ее корр. функции, и наоборот.
, можно сразу получить каноническое разложение ее корр. функции, и наоборот.
Преобразование случайных процессов
| L |
| отклик, выходная реакция |
| сист. оператор |
| ф-я воздействие, возбуждение |
1. Линейная система
 ее реакция на входные сигналы
ее реакция на входные сигналы
· Аддитивная (принципы суперпозиции)
· Однородная (принципы пропорционального подобия)
Аддитивность:

Однородность:

Примеры
· Умножение на заданную функцию:

· Дифференцирование:

· Интегрирование:

Если  c
c 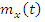 и
и 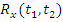 преобразуется однород. линейным оператором
преобразуется однород. линейным оператором 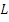 в случайную функцию
в случайную функцию 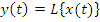 , то
, то
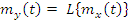
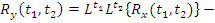
Однородное линейное преобразование применить дважды, сначала по одному аргументу, затем по другому.
2. Сложение случайных функций:
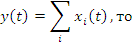
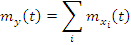
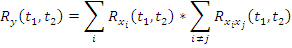
3. Умножение  на неслучайную функцию
на неслучайную функцию  :
:
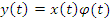
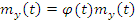

4. Частотное представление:



|
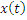


|
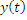


|
Связка:

Для реализации:

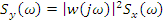

5. Функция преобразования случайных величин с точки зрения функции распределения вероятности


Область монотонности:



|
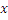
|

|



|




s w:val="24"/></w:rPr><m:t>П†</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>-1</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  – обратная функция.
– обратная функция.

|
Примеры: 
> 
Математические модели искажения сигнала шумом
1. Аддитивный шум


Сигналы и шум независимы. Исходим, что  при заданном значении
при заданном значении  . Т.е., например,
. Т.е., например,  ,
,  .
.

Т.к.

То:


В общем виде для зависимых  и
и  :
:


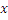
|

|
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>,</m:t></m:r></m:sup></m:sSup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t><y</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 


|

|
Многомерный случай



Пусть 

2. Мультипликативный шум


 при заданном значении
при заданном значении 



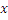
|

|
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>,</m:t></m:r></m:sup></m:sSup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t><y</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 


|

|
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>,</m:t></m:r></m:sup></m:sSup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t><y</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 


|

|

|

|



|
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>1</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 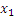


|
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>2</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 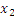


|
s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>31</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 


|

3. Влияние шума (искажения) при передаче квантованных (дискретных по значению) сигналов
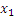
|
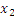
|
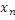
|

|

|

|
Наиболее общая характеристика (модель) – матрица вероятностей совместного появления сигналов 


Формула Байеса:

Специальные (типовые) виды (модели) случайных сигналов
1. Белый шум (аналог белого света = ∑ всех спектральных составляющих, имеющих одну интенсивность). Белый шум = ∑ гармонических колебаний всех частот, имеющих одну и ту же дисперсию амплитуды.
 – ст. белый шум
– ст. белый шум
 – нест. белый шум
– нест. белый шум


Приближенный аналог белого шума:

|
 – дискретный белый шум. Значения
– дискретный белый шум. Значения  на различных интервалах
на различных интервалах  - независимы.
- независимы.











Обозначим  , если
, если  и при этом
и при этом  возрастает так, чтобы
возрастает так, чтобы  , то
, то

2. Ограниченный по полосе белый шум


|

|

|

|

|

3. RC-шум - результат прохождения белого шума через RC-цепь (апериодическое звено)

|

|

|


4. Гауссовский шум – результат ∑ статически независимых белых шумов:


Эффективный интервал корреляции  :
:

Эффективная ширина спектра:









5. Гауссовские случайные сигналы (процессы) – 
Для любого набора  все распределения вероятностей подчиняются нормальному закону, в том числе многомерные.
все распределения вероятностей подчиняются нормальному закону, в том числе многомерные.
Композиция гауссовских процессов порождает гауссовский процесс. Плотность вероятности любых сечений  :
:

Гауссовский процесс однозначно определяется  и
и 
Многомерное нормальное распределение:

Где  ;
;  ;
; 


 – матрица алгебраических дополнений.
– матрица алгебраических дополнений.
Частный случай – случай независимых отсчетов. s w:val="24"/></w:rPr><m:t>R</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>x</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  , следовательно, преобразуется в диагональную матрицу:
, следовательно, преобразуется в диагональную матрицу:




 - строка,
- строка,  – столбец.
– столбец.

Для стационарных и эргодических процессов  .
.



Следовательно, для любого нормального процесса его любая характеристика может быть определена по  и
и 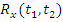



Нормальный случайный процесс полностью определяется своим математическим ожиданием и корреляционной функцией, которые могут быть вычислены по двумерной функции распределения.
Для случайного процесса с независимыми значениями (отсчетами) достаточно задания одномерного закона распределения.
Любое линейное преобразование нормального процесса распределено нормально.
6. Случайный телеграфный сигнал.
Случайный телеграфный сигнал – это сигнал 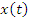 , который меняет свои значения в случайные и независимые моменты времени, а внутри интервалов времени сохраняет значения
, который меняет свои значения в случайные и независимые моменты времени, а внутри интервалов времени сохраняет значения  .
.
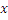
|
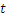
|

|

|
Случайный параметр – значение 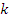 переменного знака сигнала за интервал
переменного знака сигнала за интервал 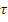 . Этот параметр распределен по закону Пуассона:
. Этот параметр распределен по закону Пуассона:

 – интенсивность переключений.
– интенсивность переключений.
Моменты переключений не зависят от текущего и будущего поведения процесса. Вероятность того, что не произойдет ни одного изменения состояния:

Вероятность того, что изменение произойдет хотя бы один раз:

Интервал времени 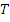 между последовательными изменениями есть случайная величина с плотностью распределения и математическим ожиданием соответственно:
между последовательными изменениями есть случайная величина с плотностью распределения и математическим ожиданием соответственно:

Для телеграфного сигнала (он полностью определен процессом Пуассона) и при этом стационарен и эргодичен:




t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/><w:lang w:val="EN-US"/></w:rPr><m:t>=ПЂ</m:t></m:r><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>О»</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
Вывод:

Произведение  в зависимости от совпадения знаков.
в зависимости от совпадения знаков.

7. Синусоидальный случайный процесс:

a)  ,
,  – случ. и равно-распр. на
– случ. и равно-распр. на 
 ,
,

Процесс стационарен и эргодичен.
b)  ,
,  - случайная величина с
- случайная величина с 
 ,
,

Процесс стационарен, но в целом не эргодичен.
8. Марковские сигналы (процессы без последействия)
Введем обозначение:  . Дискретный или непрерывный случайный процесс
. Дискретный или непрерывный случайный процесс  называется Марковским, если для любого набора
называется Марковским, если для любого набора  .
.

т.е. если для  , то значение
, то значение  ничего не добавляет (никакой информации) для определения распределения
ничего не добавляет (никакой информации) для определения распределения  . Т.е. Марковский процесс определяется своим распределением вероятности второго порядка и, следовательно, может быть задан распределением вероятности первого порядка + вероятностями перехода.
. Т.е. Марковский процесс определяется своим распределением вероятности второго порядка и, следовательно, может быть задан распределением вероятности первого порядка + вероятностями перехода.
Дискретный Марковский процесс с дискретным временем называют цепью Маркова. Цепь Маркова имеет вид:

s w:val="24"/></w:rPr><m:t> x</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>i</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  – случайная величина, принимающая значения из множества
– случайная величина, принимающая значения из множества 
Марковские цепи есть модель схемы независимых испытаний, когда существует зависимость исхода любого состояния только от исхода предыдущего.
Имеем систему с дискретными состояниями. Если система в момент времени 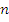 (т.е. s w:val="24"/></w:rPr><m:t>t</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>n</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
(т.е. s w:val="24"/></w:rPr><m:t>t</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>n</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  ) находилась в состоянии
) находилась в состоянии  , то вероятность перехода в состояние
, то вероятность перехода в состояние 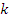 в момент
в момент  зависит в общем случае от
зависит в общем случае от  и не зависит от того, в каких состояниях система находилась в момент времени до s w:val="24"/></w:rPr><m:t>t</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>n</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
и не зависит от того, в каких состояниях система находилась в момент времени до s w:val="24"/></w:rPr><m:t>t</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>n</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 

Следовательно, цепь Маркова определяется через условные вероятности того, что система осуществит длинный переход.
Цепь Маркова называется однородной, если переходные вероятности не зависят от времени, т.е.

Обозначим  - вероятность перехода за один шаг. Тогда цепь Маркова будет описываться матрицей переходных вероятностей:
- вероятность перехода за один шаг. Тогда цепь Маркова будет описываться матрицей переходных вероятностей:

Матрица квадратная, неотрицательная, ∑ вероятностей по любой строке =1.
Многошаговые переходные вероятности.
Необходимо определить вероятность перехода системы из состояния  в состояние
в состояние 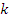 за
за 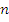 шагов. Цепь однородна.
шагов. Цепь однородна.

Оказывается, что для нахождения  достаточно знать матрицу одношаговых переходов
достаточно знать матрицу одношаговых переходов  . Покажем это.
. Покажем это.
Вводим промежуточный момент (шаг)  :
:  и будем рассматривать переход из
и будем рассматривать переход из  в
в 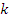 в два этапа:
в два этапа: 
 в
в  за
за  шагов,
шагов,
 в
в 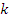 за
за  ) шагов.
) шагов.
Тогда из формулы полной вероятности:

Следовательно элемент матрицы, полученный как произведение  и
и  , т.е.
, т.е.
 - уравнение Колмогорова-Чепмена.
- уравнение Колмогорова-Чепмена.
Т. матрица переходных вероятностей за 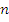 шагов и
шагов и  ) шагов.
) шагов.
Пусть  , то:
, то:

Если  :
:
 и т.д.
и т.д.
т.е.: 
Если представить исходное распределение вероятностей состояний системы в виде матрицы-строки:
 ,
,
то вероятности состояний системы в момент времени 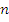 :
:

Можно получить из уравнения:

Марковские модели содержат полную информацию о двумерном законе распределения.
Пример Марковского процесса:

|
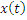
|
бел.
шум

|


Марковский процесс 2-го порядка:
| лин. опер. |
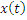
|

|
| 2-го пор. |


Зафиксируем  ,
,  . Решение определяется уравнением:
. Решение определяется уравнением:
 ,
, 
Т.е. от прошлого  не зависит. Для линейных операторов второго порядка – нет, для определения состояния при
не зависит. Для линейных операторов второго порядка – нет, для определения состояния при  необходимо знать не только
необходимо знать не только  , но и, например,
, но и, например,  .
.
Классификация состояний
Смежные состояния – возможен переход за один шаг. Граф состояния системы:
| 0 |
| 1 |
| 2 |
| P00 |
| P10 |
| P22 |
| P12 |
| P01 |
| P11 |
Вершины графа на рисунке – это состояния (все – вершины на шаге 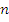 ), дуги – направление и вероятность перехода между смежными состояниями.
), дуги – направление и вероятность перехода между смежными состояниями.
Для построения графа Марковской цепи удобно использовать матрицу смежности.

Состояние  достигнуто из состояния
достигнуто из состояния  , если
, если  такое, что
такое, что  .
.
Пользуясь графовым представлением Марковского процесса, легко определить множества состояний, достижимых из фиксированного состояния  . Для этого нужно найти матрицу достижимости
. Для этого нужно найти матрицу достижимости  , где
, где  - единичная матрица,
- единичная матрица, 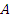 - матрица смежности.
- матрица смежности.
Состояния  и
и  называются сообщающимися, если
называются сообщающимися, если  такое
такое  и
и  , что
, что  . Состояние
. Состояние  называют несущественным, если
называют несущественным, если  такое состояние
такое состояние  , которое достижимо из
, которое достижимо из  , но состояние
, но состояние  недостижимо из
недостижимо из  .
.

|

|
Все существующие состояния цепи естественно разбиваются на классы так, что все состояния принадлежащие одному классу, сообщаются, а разным классам – не сообщаются.
Цепь Маркова называется неприводимой, если существует (ей соответствует) единственный класс сообщающихся состояний.
Подмножество С состояний цепи Маркова называют замкнутым если никакое состояние вне С не может быть достигнуто ни из какого состояния, входящего в С.
| C |
Отражающий экран:
Поглощающий экран:
Эргодические цепи Маркова.
При 
 становится независимой от состояний
становится независимой от состояний  и стремится к предельной вероятности:
и стремится к предельной вероятности:
ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
Распределение  называется стационарным распределением вероятностей эргодической цепи Маркова, т.е. s w:val="24"/></w:rPr><m:t>u</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>k</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w
называется стационарным распределением вероятностей эргодической цепи Маркова, т.е. s w:val="24"/></w:rPr><m:t>u</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>k</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w
|
|
 2018-02-14
2018-02-14 304
304







