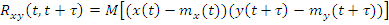
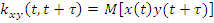

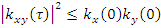
Произвольная функция, не обладает свойством четности или нечетности.
Если один из процессов центрированный, то 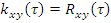
Коэффициент корреляции двух процессов характеризует степень линейной зависимости процессов при сдвиге τ:
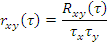
Статистическая зависимость для двух случайных величин: мера их линейной статистической связи – коэффициент корреляции s w:val="24"/></w:rPr><m:t>ПЃ</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/><w:lang w:val="EN-US"/></w:rPr><m:t>xy</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 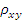 :
:
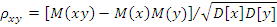
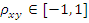
В частном случае, если 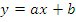 , то
, то 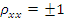 .
.
При 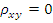 случайная величина некоррел., т.е.
случайная величина некоррел., т.е.
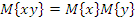
Линейные преобразования случайных функций.
1. Если  c
c 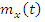 и
и 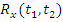 преобразуется однород. линейным оператором
преобразуется однород. линейным оператором 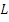 в случайную функцию
в случайную функцию 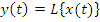 , то
, то
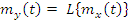
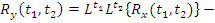
Однородное линейное преобразование применить дважды, сначала по одному аргументу, затем по другому.
2. Сложение случайных функций:
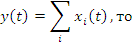
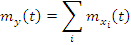
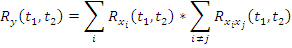
3. Умножение  на неслучайную функцию
на неслучайную функцию  :
:
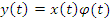
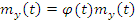

4. Стационарная линейная система с частотной характеристикой 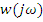 :
:
| w(s) |
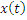
|
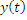
|
Если 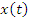 – детерминированная функция, то
– детерминированная функция, то 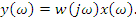
Если 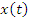 – случайная функция, то
– случайная функция, то 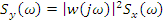
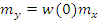
New Version
Эффективный интервал корреляции
Нормирование случайных процессов и корр. функции.
1. Нормированная случайная функция:
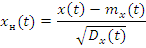
· 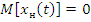
· Центрированная
· 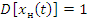
2. Нормированая корр. функция:
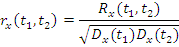
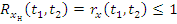
3. Эффективный интервал корр.:
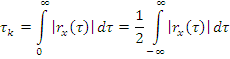
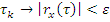
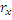
|
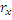
|
| 1 |
| t |
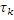
|
| 1 |
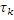
|
| t |
Эффективная ширина спектра
| ωt |
| ft |
| Sx |
| fm |
| Fk |
| ∆f |
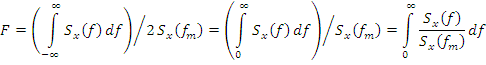
Аналогично для 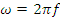 .
.
 2018-02-14
2018-02-14 315
315








