НЕВЯЗКОЙ ЖИДКОСТИ
В данном параграфе установим общие закономерности движения невязкой жидкости. Для этого в потоке невязкой жидкости выделим элементарный объем в виде параллелепипеда с ребрами dx, dy, dz, параллельными координатным осям (рис.4.4).

Рис. 4.4. Схема к выводу дифференциальных уравнений
движения невязкой жидкости
На массу жидкости в объеме параллелепипеда, равную  действуют массовые силы, пропорциональные массе, и поверхностные силы давления окружающей жидкости, распределенные по граням параллелепипеда, перпендикулярные к ним и пропорциональные площадям соответствующих граней.
действуют массовые силы, пропорциональные массе, и поверхностные силы давления окружающей жидкости, распределенные по граням параллелепипеда, перпендикулярные к ним и пропорциональные площадям соответствующих граней.
Обозначим через 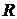 плотность распределения равнодействующей массовых сил и через
плотность распределения равнодействующей массовых сил и через  ,
, 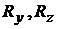 - ее проекции на соответствующие оси координат. Тогда проекция на направление ОХ массовых сил, действующих на выделенную массу жидкости, равна
- ее проекции на соответствующие оси координат. Тогда проекция на направление ОХ массовых сил, действующих на выделенную массу жидкости, равна  .
.
Обозначим через р - давление в произвольной точке с координатами x, y, z, являющейся одной из вершин параллелепипеда. Пусть это будет точка А на рис.4.4.
В силу сплошности жидкости и непрерывности функции давления р = f (x, y, z, t) в точке В с координатами (х + dx, y, z) давление будет равно  с точностью до бесконечно малых второго порядка.
с точностью до бесконечно малых второго порядка.
Разность давлений равна  и будет одинаковой для любой пары выбранных на гранях точек с одинаковыми координатами у и z.
и будет одинаковой для любой пары выбранных на гранях точек с одинаковыми координатами у и z.
Проекция на ось ОХ результирующей силы давления равна  . Запишем уравнение движения в направлении оси ОХ
. Запишем уравнение движения в направлении оси ОХ
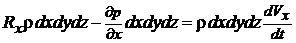 (4.14)
(4.14)
или после деления на массу  получим
получим
 . (4.15)
. (4.15)
Аналогично получим уравнения движения в направлении осей OY и OZ. Тогда система дифференциальных уравнений движения невязкой жидкости имеет вид
 (4.16)
(4.16)
Эти дифференциальные уравнения были впервые получены Л. Эйлером в1755 г.
Члены этих уравнений представляют собой соответствующие ускорения, а смысл каждого из уравнений заключается в следующем: полное ускорение частицы вдоль координатной оси складывается из ускорения от массовых сил и ускорения от сил давления.
Уравнения Эйлера в таком виде справедливы как для несжимаемой, так и для сжимаемой жидкости, а также для случая, когда наряду с силой тяжести действуют другие массовые силы при относительном движении жидкости. При этом в величины Rx, Ry и Rz должны войти компоненты ускорения переносного (или поворотного) движения. Так как при выводе уравнений (4.6) не накладывались условия стационарности движения, то они справедливы и для неустановившегося движения.
Учитывая, что для неустановившегося движения компоненты (проекции) скорости V являются функциями времени, можно записать ускорение выделенной массы жидкости в развернутом виде:
 . (4.17)
. (4.17)
Так как  уравнения Эйлера (4.16) можно переписать в виде
уравнения Эйлера (4.16) можно переписать в виде
 . (4.18)
. (4.18)
Для случая покоящейся жидкости  уравнения (4.16) совпадают с дифференциальными уравнениями равновесия жидкости (2.5).
уравнения (4.16) совпадают с дифференциальными уравнениями равновесия жидкости (2.5).
В задачах динамики жидкости массовые силы обычно считаются заданными (известными). Неизвестными являются функции давления
р = f (x,y,z,t), проекции скорости Vx = f (x, y, z, t), Yy = f (x, y, z, t),
Vz = f (x, y, z, t) и плотность r = f (x, y, z, t), т.е. всего пять неизвестных функций.
Для определения неизвестных переменных используется система уравнений Эйлера. Поскольку число неизвестных превышает число уравнений к системе Эйлера добавляют уравнение неразрывности и уравнение состояния среды.
Для несжимаемой жидкости уравнение состояния p = const и уравнение неразрывности
 . (4.19)
. (4.19)
Профессором Казанского университета И.С.Громекой в 1881 г. уравнения Эйлера были преобразованы и записаны в иной форме. Рассмотрим уравнения (4.18).
В первом из них вместо  и
и  подставим их выражения из (3. 13):
подставим их выражения из (3. 13):

 и
и  . (4.20)
. (4.20)
Тогда
 . (4.21)
. (4.21)
Приняв обозначение  , можем записать
, можем записать

 . (4.22)
. (4.22)
Аналогично преобразовав два остальных уравнения системы (4.7), получим систему уравнений в форме, данной Громекой
 (4.23)
(4.23)
Если действующие на жидкость массовые силы обладают потенциалом, то проекции плотности распределения массовых сил Rx, Ry, Rz представляются частными производными от потенциальной функции П:
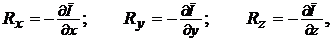 (4.24)
(4.24)
откуда
- dП = Rxdx + Rydy + Rzdz .(4.25)
Подставив значения Rx, Ry, Rz в систему (4.8), получим систему дифференциальных уравнений движения несжимаемой жидкости под действием сил, имеющих потенциал:
 (4.26)
(4.26)
При установившемся движении частные производные составляющих скорости по времени равны нулю:
 . (4.27)
. (4.27)
Тогда уравнения системы (4.10) примут вид
 (4.28)
(4.28)
Умножив каждое из уравнений системы (4.11) на соответствующие проекции элементарного перемещения, равные dx = Vxdt; dy = Vydt;
dz = Vzdt, и сложим уравнения. Будем иметь
 Правую часть полученного выражения можно переписать в виде определителя, т.е.
Правую часть полученного выражения можно переписать в виде определителя, т.е.
 (4.29)
(4.29)
Если определитель равен нулю, т.е.
 (4.30)
(4.30)
то имеем
 . (4.31)
. (4.31)
Это уравнение Бернулли для элементарной струйки при установившемся движении невязкой жидкости.
Чтобы привести уравнение (4.14) к виду уравнения Бернулли, полученному в (4.1), определим вид потенциальной функции П для случая, когда действует только одна массовая сила - сила тяжести. В этом случае Rx = Ry = 0 и Rz = - g (ось OZ направлена вверх). Из (4.9) имеем
 или
или  . (4.32)
. (4.32)
Подставив это выражение П в (4.14), получим
 или
или  .
.
Последнее выражение полностью соответствует уравнению Бернулли (4.4).
Выясним, в каких случаях установившегося движения невязкой несжимаемой жидкости справедливо уравнение Бернулли или, иначе говоря, в каких случаях определитель в правой части уравнения (4.13) обращается в нуль.
Известно, что определитель равен нулю, если две строки (или два столбца) равны или пропорциональны друг другу или если одна из его строк или один из столбцов равны нулю. Рассмотрим эти случаи последовательно.
А. Пропорциональны члены первой и третьей строк, т.е. уравнение Бернулли справедливо, если
 .
.
Это условие выполняется на линиях тока (3.2).
Б. Пропорциональны члены первой и второй строк, т.е. уравнение Бернулли справедливо, если
 .
.
Это условие выполняется на вихревых линиях (3.16).
В. Пропорциональны члены второй и третьей строк:
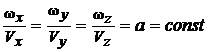 . (4.16)
. (4.16)
Тогда ωx= a Vx; ωy = a Vy; ωz = a Vz.
 2018-02-14
2018-02-14 855
855








