Потенциальная яма с бесконечно высокими стенками. Рассмотрим одномерный случай. Потенциальная энергия имеет вид

                                      
где l – ширина ямы, а энергия отсчитывается от ее дна.

Уравнение Шредингера для стационарных состояний запишется в виде

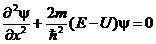                                     .                                              (7)
По условию задачи (бесконечно высокие стенки), частица не проникает за пределы ямы, поэтому вероятность ее обнаружения за пределами ямы равна нулю. Следовательно, на границах ямы волновая функция должна обращаться в ноль

                                            .                                                    (8)
В пределах ямы () уравнение Шредингера сводится к уравнению

                                          .                                                  (9)
Общее решение уравнения (9) имеет вид

                                        ,
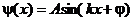где , A и j – произвольные постоянные.

Граничные условия (8) будут выполнены при  и , где n – целое число. Отсюда следует, что энергия частицы принимает квантованные значения

                                .
Значения энергии  называются уровнями энергии, а число n, определяющее энергетические уровни частицы, называется главным квантовым числом.

Собственные волновые функции частицы имеют вид

                                          .
Постоянная A найдется из условия нормировки

                                         .
В результате интегрирования получим 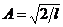, а собственные волновые функции будут иметь вид

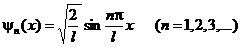                                                             (10)

Туннельный эффект. Рассмотрим потенциальный барьер прямоугольной формы для одномерного (по оси x) движения частицы

                                      
Классическая частица, обладая энергией E, либо беспрепятственно пройдет над барьером (при 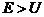), либо отразится от него (при ), т.е. она не может проникнуть сквозь барьер. Для микрочастицы же, даже при 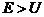, имеется отличная от нуля вероятность отразиться от барьера. При  имеется также отличная от нуля вероятность прохождения частицей барьера. Подобные выводы следуют из решения уравнения Шредингера.

Уравнение Шредингера для стационарных состояний для каждой из выделенной на рис. области имеет вид

для областей 1, 3 , ,

для области 2         ,  .
Общее решение этих дифференциальных уравнений

                      (для области 1);                             (11а)

                      (для области 2);                            (11б)

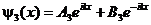                       (для области 3).                            (11в)
В выражениях для областей 1 и 3 (k – действительное число) первый член представляет собой правую плоскую волну (соответствует частице, движущейся в положительном направлении x), а второй – левую волну (соответствует частице, движущейся в отрицательном направлении x). Коэффициент  следует положить равным нулю, поскольку из физического смысла в области 3 имеется только волна, прошедшая сквозь барьер и распространяющаяся слева направо. Интерес представляет случай, когда полная энергия частицы меньше высоты барьера, поскольку при  законы классической физики не разрешают частице проникнуть через барьер. В этом случа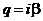е , где , является чисто мнимым числом.

Для описания туннельного эффекта вводится понятие коэффициента прозрачности D потенциального барьера. Он равен отношению плотности потока прошедших частиц к плотности потока падающих

                                           .

Условие непрерывности волновой функции и ее производных позволяют найти связь между коэффициентами в уравнениях (11а)-(11в) и определить коэффициент прозрачности. Для малых значений коэффициента получается зависимость

                               ,                                      (12)
где  – постоянный множитель, близкий к единице.