По аналогии с классической механикой закон движения микрочастицы должен определяться законом распространения волн де Бройля. Распространение любой волны описывается волновым уравнением. Уравнение плоской волны, распространяющейся вдоль оси 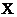 (одномерный случай):
(одномерный случай):
 .
.
Выразив  и
и 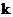 через энергию и импульс частицы, мы получим
через энергию и импульс частицы, мы получим  – волновую функцию для свободной частицы, которой соответствует волна с частотой
– волновую функцию для свободной частицы, которой соответствует волна с частотой  и волновым числом
и волновым числом  , т.е.
, т.е.  . Учитывая, что
. Учитывая, что 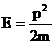 , выразим
, выразим  и
и 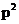 из уравнения плоской волны. Тогда
из уравнения плоской волны. Тогда
 и
и  .
.
Подставляя  и
и 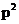 в уравнение
в уравнение 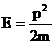 , получим:
, получим:  =
=  .
.
В трехмерном случае, т.е. когда  , волновое уравнение:
, волновое уравнение:
 или
или  ,
,
где  – оператор Лапласа. Это волновое уравнение Шредингера для свободной частицы.
– оператор Лапласа. Это волновое уравнение Шредингера для свободной частицы.
Если микрочастица движется в силовом поле, т.е. имеет потенциальную энергию  , то уравнение принимает вид:
, то уравнение принимает вид:
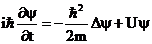 – это общее волновое уравнение Шредингера – основное уравнение нерелятивистской квантовой механики. Оно не выводится, а постулируется и справедливо для любой микрочастицы, движущейся со скоростью
– это общее волновое уравнение Шредингера – основное уравнение нерелятивистской квантовой механики. Оно не выводится, а постулируется и справедливо для любой микрочастицы, движущейся со скоростью 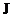 <<
<<  .
.
 2018-02-14
2018-02-14 399
399








