Уравнение Шредингера для стационарных состояний

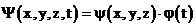Если силовое поле, в котором движется частица, стационарно, то потенциальная энергия частицы не зависит от времени. Тогда функцию можно представить: и уравнение Шредингера для частицы, движущейся вдоль оси 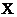(одномерный случай):

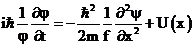Видно, что левая часть зависит только от времени, а правая – только от координаты, причем обе части равны друг другу только тогда, когда каждая из сторон равна – полной энергии частицы. Тогда, приравнивая каждую часть к , получим два уравнения:

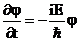; (1)

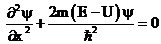. (2)

При движении частицы в пространстве уравнение (2) примет вид:

или 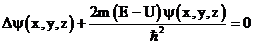– это амплитудное уравнение Шредингера для стационарных состояний. Функция

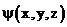называется амплитудой волновой функции

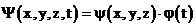Если движение происходит в ограниченной области пространства, то уравнение Шредингера имеет решение только при строго определенных значениях энергии , которые называются собственными, а функции 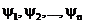, соответствующие энергиям называются собственными волновыми функциями. Уравнение (2): 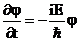имеет решение , где 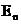– одно из собственных значений энергии (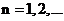). Поставив 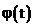в волновую функцию, получим:

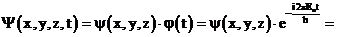
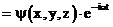, т.к. 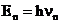, а .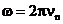

Принцип причинности в квантовой механике – задание волновой функции 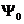в момент времени 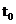определяет ее значение 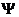в последующие моменты времени путем решения уравнения Шредингера. В квантовой механике задание функции 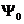– причина, а состояние 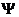в последующие моменты – следствие.