Рассмотрим одномерную (движение вдоль оси 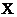 ) прямоугольную потенциальную яму шириной
) прямоугольную потенциальную яму шириной 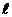 с бесконечно высокими стенками. Такая яма описывается потенциальной энергией вида:
с бесконечно высокими стенками. Такая яма описывается потенциальной энергией вида:
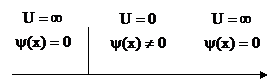 |



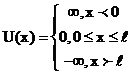
О 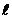
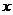
Уравнение Шредингера для стационарных состояний:
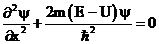 .
.
По условию частица не проникает за пределы ямы, поэтому волновая функция за пределами равна нулю и граничное условие: 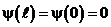 . В пределах ямы
. В пределах ямы 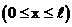 уравнение Шредингера
уравнение Шредингера 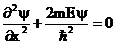 , но
, но 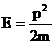 , а
, а 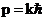 , тогда
, тогда 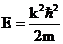 и
и 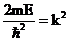 , т.е.
, т.е. 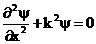 .
.
Общее решение уравнения Шредингера:
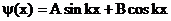 .
.
Поскольку при 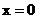 ,
, 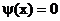 , то
, то 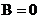 , тогда
, тогда 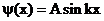 . Условие
. Условие 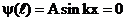 выполняется только при
выполняется только при 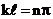 , где
, где 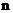 – целое число. Волновое число
– целое число. Волновое число 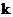 должно удовлетворять условию
должно удовлетворять условию 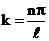 . Тогда энергия частицы
. Тогда энергия частицы 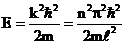 (n = 1,2,3,.,) Значит уравнение Шредингера, описывающее движение частицы в потенциальной яме, удовлетворяется только при собственных значениях энергии
(n = 1,2,3,.,) Значит уравнение Шредингера, описывающее движение частицы в потенциальной яме, удовлетворяется только при собственных значениях энергии 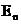 , зависящих от числа
, зависящих от числа 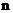 . Энергия частицы в потенциальной яме принимает только определенные дискретные значения, т.е. квантуется. Квантовые значения энергии называются уровнями энергии, а число
. Энергия частицы в потенциальной яме принимает только определенные дискретные значения, т.е. квантуется. Квантовые значения энергии называются уровнями энергии, а число 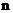 – главным квантовым числом.
– главным квантовым числом.
Подставив в 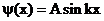 значение
значение 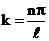 , найдем собственные функции
, найдем собственные функции 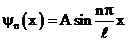 . Константу
. Константу 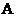 найдем из условия нормировки:
найдем из условия нормировки:

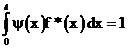 или
или 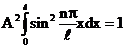 .
.
Интеграл равен:
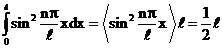 , тогда
, тогда 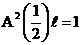 , откуда
, откуда 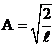 . Тогда
. Тогда 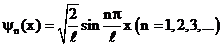 .
.
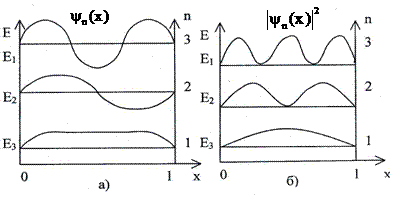
На рисунке а) приведены собственные функции, соответствующие уровням энергии при 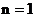 , 2 и 3. На рисунке б) изображена вероятность нахождения частицы в различных участках ямы, равная
, 2 и 3. На рисунке б) изображена вероятность нахождения частицы в различных участках ямы, равная 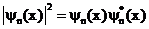 при
при 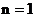 , 2 и 3. Энергетический интервал между уровнями
, 2 и 3. Энергетический интервал между уровнями
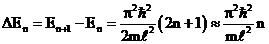 .
.
Например, для свободного электрона в металле 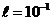 м и
м и 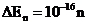 эВ, т.е. уровни расположены так близко, что спектр можно считать непрерывным. Если размер ямы соизмерим с атомным
эВ, т.е. уровни расположены так близко, что спектр можно считать непрерывным. Если размер ямы соизмерим с атомным 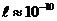 м, то
м, то 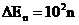 эВ, т.е. явно дискретные значения энергии (линейчатый спектр).
эВ, т.е. явно дискретные значения энергии (линейчатый спектр).
V. АТОМНАЯ ФИЗИКА
 2018-02-14
2018-02-14 309
309








