Соотношение неопределенностей

В классической механике состояние частицы, движущейся по определенной траектории, в любой момент времени однозначно определяется значением координат () и трех составляющих импульса (). Вследствие наличия у микрочастицы волновых свойств, нельзя говорить о движении частицы по определенной траектории и об одновременных точных значениях ее координаты и импульса. Так как понятие «длина волны в данной точке» лишено физического смысла.

Пусть микрочастица движется вдоль оси  с импульсом , тогда согласно формуле де Бройля ей соответствует волна с длиной . Но волна, протяженный объект, определена в диапазоне < < , поэтому интервал, в котором локализована частица 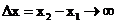. Т.е. частица, обладающая определенным импульсом , не имеет определенной координаты и наоборот.

Степень точности, с которой может быть определено положение микрочастицы в пространстве, задается соотношением неопределенностей Гейзенберга:

Это один из основных законов квантовой механики. Из него следует, что чем точнее определяется координата микрочастицы, тем неопределеннее становятся составляющие её импульса и наоборот. Отсюда также следует, что в квантовой механике утрачивается смысл понятия траектории, которое несовместимо с волновыми свойствами.