Затухающие колебания

Затухающими колебаниями называются колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшают-ся. Найдем закон движения груза в условиях предыдущей задачи, но с учетом сопротивления воздуха, которое пропорционально скорости движения.

Решение

К силам, действующим на груз, прибав­ляется здесь сила сопротивления воздуха  (знак минус показывает, что сила R направлена противопо­ложно скорости u). Тогда дифференциальное уравнение движения в проекции на ось Ox имеет вид

или если положить 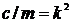, , то

                                                (3)

Это уравнение также является линейным однородным уравнением второго порядка с постоянными коэффициен­тами. Его характеристическое уравнение:

 имеет корни

                                               (4)

Характер движения целиком определяется этими кор­нями. Возможны три различных случая. Рассмотрим сна­чала случай, когда . Это неравенство имеет место, когда сопротивление среды невелико. Если поло­жить , то корни (4) имеют вид . Тогда общее решение можно записать в виде

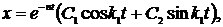
или, преобразовав, умножая и деля на , получим:

    положим, что

,

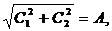
    тогда

                                                (5)

    График зависимости отклонения от положения равновесия от времени имеет вид:

Если заданы начальные условия: 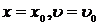 при t = 0, то можно определить А и a. Для этого находим

и подставляем t = 0 в выражения для и  получим систему уравнений

Разделелив обе части второго уравнения на соответствующие части первого получим

  откуда

или  а

    Так как

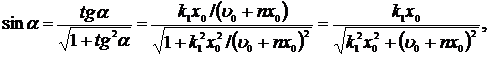
    то

Решение (5) показывает, что имеют место затухающие колебания. Действии-тельно, амплитуда колебания 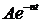 зави­сит от времени и является монотонно убывающей функцией, причем   при .

Период затухающих колебаний определяется по формуле

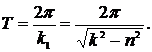
Моменты времени, в которые груз получает максималь­ное отклонение от начала координат (положения равнове­сия), образуют арифметическую прогрессию с разностью, равной полупериоду Т/2. Амплитуды затухающих коле­баний образуют убывающую геометрическую прогрессию со знаменателем, равным 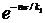 или . Эта величина называется декрементомзатухания и обычно обозначается буквой D. Натуральный логарифм декремента ln D = - пТ/2 называется логарифмическим декрементом затухания.

Частота колебаний в этом случае меньше, нежели в предыдущем (), но, как и там, не зависит от начального положения груза.

Если сопротивление среды велико и , то, положив , получим корни (4) в виде   Так как , то оба корня отрицательны. Общее решение уравнения в этом случае имеет вид

                                         (6)

Отсюда видно, что движение апериодическое и не имеет колебательного характера. Аналогичный характер будет иметь движение и в случае 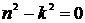, когда общее решение имеет вид

                                                 (7)

Легко заметить, что в обоих последних случаях при  имеем .

Если заданы начальные условия   и , то в случае, когда , имеем , а . Решая эту систему относительно  и , получим

,

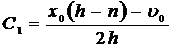       и, следовательно

 

    В случае же, когда 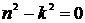, получаем ,  и следовательно,