Вынужденные колебания без учета сопротивления среды

Вынужденными колебаниями называют колебания, вызванные внешней периодической возмущающей силой.

Пусть груз весом Р подвешен на вертикальной пружине, длина которой в ненагруженном состоянии равна 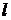. На груз действует периодическая возмущающая сила где Q и р — постоянные. Найдем закон движения груза, пренебрегая массой пружины и сопротивлением среды.

Решение

Как и для гармонических колебаний, получаем уравнение

Полагая, как и прежде, 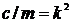и, кроме того, перепишем уравнение в виде

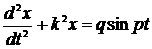(8)

Это—неоднородное линейное уравнение второго порядка с постоянными коэффициентами, причем однородным уравнением, соответствующим уравнению (8),является (1). Поэтому ; остается найти х. Если предположить, что , то частное решение х, нужно искать в виде , где М и N — коэффициенты, подлежащие определению. Итак,

Производя вычисления, получаем

откуда М =0 и Полученное таким образом частное решение

(9)

определяет так называемые вынужденные колебания, созданные возмущаю-щей силой . Вынужденные колебания, имеют тот же период, что и возмущающая сила, совпадают с ней по фазе (т. е. имеют одинаковую начальную фазу) при k>p, либо отличаются на p, если k<p, т. е. если N <0.

Закон движения представляется общим решением

. (10)

Оно слагается из собственно вынужденных колебаний (9), которые определяются внешней возмущающей силой, и собственных колебаний (2), обусловленных исключительно внутренними причинами: жесткостью пружины и массой груза.

Если заданы начальные условия: и , то можно определить произвольные постоянные А и u. Для этого продифференцируем функцию (10):

и подставим в выражения х и значение аргумента t = 0; получим систему уравнений относительно A и a:

Преобразуем её так:

возведем в квадрат обе части каждого из этих уравнений и сложим. Тогда

Для нахождения a разделим обе части первого уравнения на соответствую-щие части второго; получим

откуда

при этом ,

Итак, искомым частным решением, удовлетворяющим заданным начальным условиям, является функция

или

Частное решение (9), характеризующее собственно вынужденные колебания, было получено в предположении, что , т. е. что частота внешней силы не совпадает с частотой собственных колебаний. Если же , то дело будет обстоять совсем иначе. Действительно, уравнение (8) можно переписать теперь в виде

(11)

Частное решение следует искать в форме

где М и N — коэффициенты, подлежащие определению. Итак,

откуда получаем , , и следовательно, частное решение имеет вид

Общее решение в этом случае

(12)

Найдем и подставим в выражения х и значение t =0; получим

или

Из последних двух равенств находим

откуда

Перепишем общее решение так:

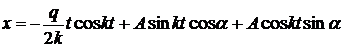
тогда искомое частное решение, удовлетворяющее заданным начальным условиям, запишется в виде.

Выражение (12) показывает, что амплитуда вынужденных колебаний 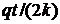в этом случае может стать неограниченно большой даже тогда, когда q невелико. Иначе говоря, возможно получение сколь угодно больших амплитуд при малых возмущающих силах. Это явление называется резонансом. Таким образом, резонанс наступает тогда, когда частота возмущающей силы совпадает с частотой собственных колебаний.

Впрочем, в действительности точное совпадение этих частот не является необходимым. Выражение (9) для вынужденного колебания показывает, что при близости частот амплитуда может быть очень большой, хотя и ограниченной при фиксированных частотах k и р. Возможностью создания колебаний с значительной амплитудой часто пользуются в различных усилителях, например в радиотехнике. С другой стороны, в большом числе случаев появление больших амплитуд является вредным, ибо может приводить к разрушению конструкций (скажем, мостов или перекрытий).

Вынужденные колебания с учетом сопротивления среды.

Найдем закон движения груза в условиях предыдущей задачи с учетом сопротивления среды, пропорционального скорости движения.

Решение

Как и выше, имеем

или положив , 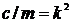и

(13)

Однородным уравнением, соответствующим (13), является уравнение (3) с корнями характеристического уравнения (4). Предположим, что сопротивление среды невелико, т. е. . При этом общее решение однородного уравнения имеет вид (5):

где . Это решение определяет свободные колебания, которые будут затухающими. Для отыскания вынужденных колебаний ищем частное решение в виде

Имеем:

Сравнивая коэффициенты, получаем систему

Так как

то

и мы находим частное решение

Преобразуем выражение следующим образом:
.

Обозначив

(14)

перепишем виде

(15)

Выражение

(16)

носит название сдвига фазы. Общее решение, как и в предыдущей задаче, слагается из свободных колебаний [см. формулу (5)]исобственно вынужденных колебаний (15):

(17)

Первое слагаемое, как было сказано выше, определяет затухающие колебания, которые, особенно при большом , довольно скоро становятся мало ощутимыми. Что касается вынужденных колебаний (15), то их амплитуда (14) не зависит от времени и пропорциональна амплитуде Q периодического возмущения, так как . Онаотличается от q множителем

(18)

характеризующим зависимость амплитуды вынужденного колебания от частоты возмущающей силы.

Определим максимум этой амплитуды. Для этого найдем производную функции (18)

Положив , получим уравнение (случай р = 0 отбрасывается как невозможный), корень которого дает частоту внешних сил:

при которой, как показывает проверка достаточных условий экстремума, амплитуда вынужденных колебаний будет максимальной. Максимальное значение амплитуды равно

(19)

Формула (19) показывает, что амплитуда колебаний тем больше, чем меньше п. При малых п частота р близка к частоте собственных колебаний k.

Решение (15) существует всегда, когда

В случае получаем p=k и n = 0, и уравнение (13) превращается в уравнение (11). Здесь вновь наступает явление резонанса, при котором, как было рассмотрено выше, вынужденные колебания имеют вид (12).