2018-02-14
803
Ход работы
Имеются следующие исходные данные:
Таблица 1
Исходные данные
| Y | X |
| 12,110 | 3,650 |
| 12,300 | 3,820 |
| 13,820 | 3,760 |
| 14,840 | 5,240 |
| 15,860 | 5,030 |
| 16,410 | 5,520 |
| 17,800 | 5,620 |
| 18,610 | 6,980 |
| 19,570 | 6,910 |
| 21,260 | 7,950 |
| 21,080 | 7,240 |
| 22,990 | 9,270 |
| 23,430 | 8,460 |
| 24,630 | 10,300 |
| 25,410 | 10,720 |
|
| 10,050 |
Где 
- прогнозное значение фактора x.
Исходные данные формируются в первых двух столбцах A3:B17. Блок промежуточный данных – C3:Q17. Прогнозные значения вычисляются в 18 ряде.
Для нахождения средних значений столбцов отводим 21 ряд. Используем встроенную функцию СРЗНАЧ.
Для нахождения сумм столбцов отводим 24 ряд и используем встроенную функцию СУММ.
Нахождение оценок параметров
Для вычисления теоретической регрессии, которая имеет следующий вид:
необходимо вычислить параметры модели – а,b.
Параметры модели вычисляются по формулам:
Значение параметра а находится в ячейке В31. Формула имеет вид =(B21*A21-C21)/(B21^2-E21)
a= 1,868585;
Значение параметра b находится в ячейке В32. Формула имеет вид =A21-B21*B31
b= 6,158884
Также найдем оценки параметров с помощью функции ЛИНЕЙН(A3:A17;B3:B17;1;1).
Таблица 2
Результат работы функции ЛИНЕЙН
 |  |
 |  |
 | S |
 | Степени свободы |
| SST | SSE |
Таблица 3
Результат работы функции ЛИНЕЙН для данной задачи
| 1,868585 | 6,158884 |
| 0,106409 | 0,751154 |
| 0,959548 | 0,918571 |
| 308,3679 | 13 |
| 260,1921 | 10,96903 |
Расчет теоретических значений У
Рассчитываем теоретические значения У по формуле 
в ячейках F3:F17. В ячейку F3 вводим формулу =$B$31*B3+$B$32.
Для прогнозного значения х16= 10,050 найдем значение y по формуле ур=а* хр+b
ур= 24,938.
Выяснение тесноты связи между у и х
Для выяснения тесноты связи можно воспользоваться двумя методами:
-построение точечной даиграммы:
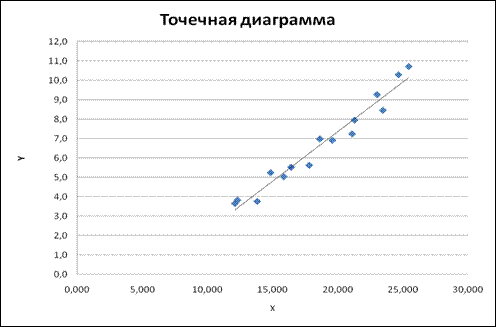
Рис.1 – Точечная диаграмма
- использование коэффициента корреляции r
(-1<=r<=1)
Для нахождения коэффициента корреляции можно воспользоваться следующими формулами:
- Встроенная функция Excel КОРРЕЛ(A3:B17);
r1= 0,979565
- Линейный коэффициент корреляции:
а)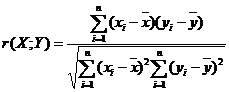 
r2= 0,979565
б) 
r3= 0,979565
Так как коэффициент корреляции при вычислении всеми тремя способами равен r=0,979565, то между у и х наблюдается тесная линейная связь.
Нахождение коэффициента детерминации
Для парной линейной регрессии: 
Значение коэффициента детерминации находится в ячейке В34 и В35.
=0,959548 при вычислении первым и вторым способом.
Индекс корреляции 
, R=0,97956 находится в ячейке B36.
Статистическая значимость коэффициентов
Рассчитывается t-статистика Стьюдента:
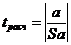
Значение tрасч находится в ячейке В38.
tрасч =17,56041
В ячейку В37 tкрит находится при помощи встроенной функции СТЬЮДРАСПОБР (0,025;13)
tкрит = 2,532638;
Если 
,то параметр а статистически значимый.
