Закон распределения по скоростям и по компонентам скоростей Максвелла. Скорости теплового движения(средняя арифметическая, средняя квадратичная, наиболее вероятная)

Рассмотрим газ, находящийся в состоянии равновесия. При этом в нем устанавливаются постоянные давление и температура. Молекулы газа движутся беспорядочно, сталкиваясь между собой и со стенками сосуда, беспрерывно меняя свою скорость. Все направления скорости равновероятны, а сами скорости – различны. Будем считать, что все возможные скорости заключены в интервале от 0 до ∞. В реальных системах мало молекул с очень малыми скоростями, а верхний предел ограничен хотя бы потому, что число молекул N, хотя и велико, но конечно,следовательно, полная энергия системы и скорость любой молекулы также конечны.

Поскольку величина скорости принимает непрерывный ряд значений, то бессмысленно ставить задачу об определении числа молекул, точно имеющих ту или иную скорость, – число таких молекул равно нулю, потому что число молекул конечно, а возможных значений скорости бесконечно много. Корректная постановка задачи может быть такой: сколько молекул (или какая их доля) имеют скорость в промежутке от v до v+Δv? Пусть Δ N – число молекул с такими скоростями. Очевидно, что:

1) чем больше интервал Δv, тем больше Δ N;

2) Δ N зависит от самой скорости v, так как молекул с одним значением скорости больше, с другим – меньше;

3) чем больше полное число молекул N, тем больше Δ N.

Тогда , где коэффициент пропорциональности  сам является функцией скорости: 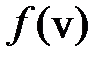. Доля молекул со скоростями, лежащими в интервале , равна . При достаточно большом числе молекул она равна вероятности  того, что : . И, наконец, будем неограниченно уменьшать интервал ; тогда

.                                   (6.38)

Это соотношение позволяет сформулировать физический смысл функции распределения Максвелла по скоростям: функция распределения численно равна доле молекул (вероятности) того, что молекула имеет скорость в промежутке , в расчёте на единичный интервал скоростей