В. Распределение по модулю скорости

Значения компонент скорости независимы. Тогда по теореме об умножении вероятностей вероятность того, что молекула одновременно имеет компоненты скорости, лежащие в интервалах

,

,

,

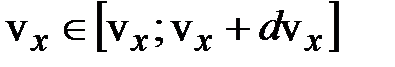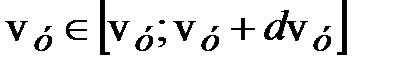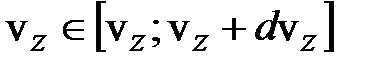равна произведению соответствующих вероятностей:

.

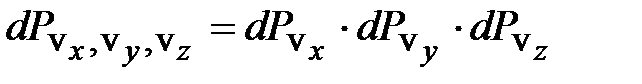Из (6.40) и (6.41):

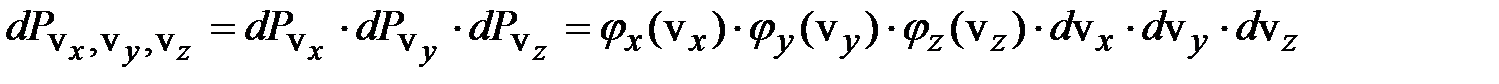
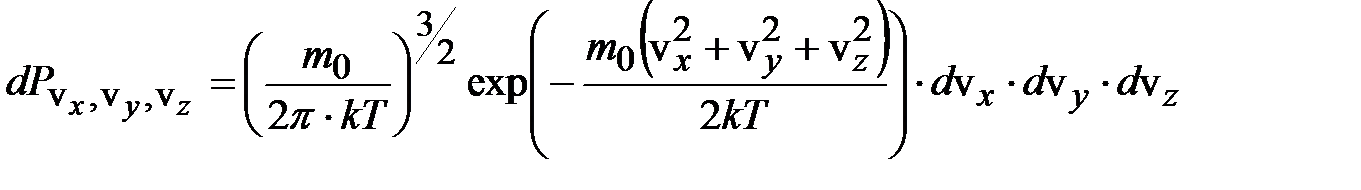
По теореме Пифагора 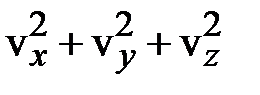 есть квадрат скорости молекулы 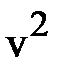, тогда

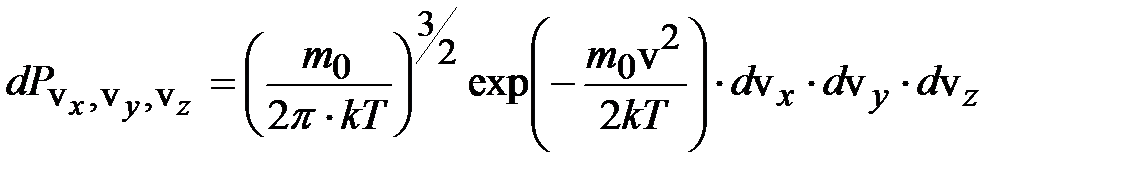.            (6.43)

Вероятность 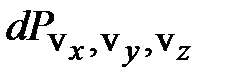отличается от вероятности  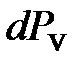того, что модуль скорости 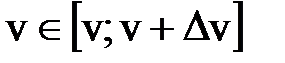, так как  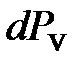зависит только от модуля скорости, а при одном и том же значении скорости  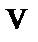проекции её могут принимать множество различных значений, лишь бы выполнялось равенство .

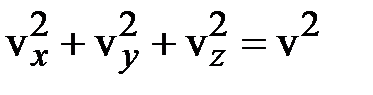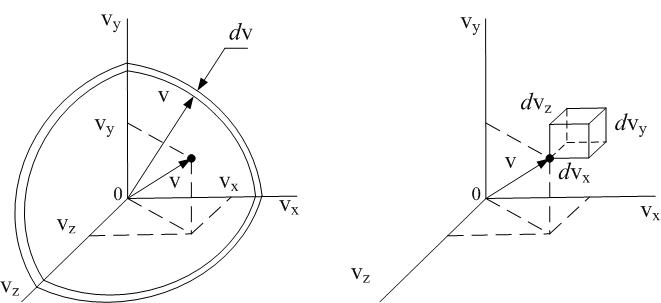
Рис.6.8

а

б

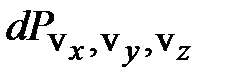Соотношение между и 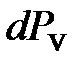 можно найти, если рассмотреть пространство скоростей: каждой молекуле в нём соответствует точка, координаты которой равны проекциям скорост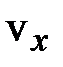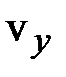и ,  и 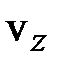 (рис.6.8).

Распределение точек в пространстве скоростей сферически симметрично относительно начала координат; плотность точек зависит только от модуля скорости v. Нас интересуют молекулы, скорости которых лежат в интервале 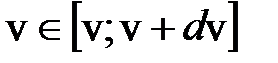. В пространстве скоростей им соответствует сферический слой радиусом v и толщиной d v. Число точек 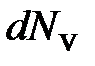, лежащих в этом слое (а также молекул, модуль скорости которых 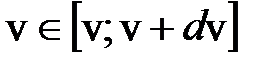), пропорционально объёму слоя 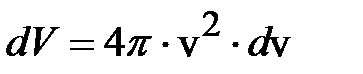(рис.6.8,а) и полному числу молекул; вероятность  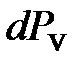также пропорциональна 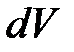. Коэффициент пропорциональности между вероятностью и соответствующим элементарным объёмом в пространстве скоростей уже найден в соотношении (6.43): там элементарным объёмом было произведение  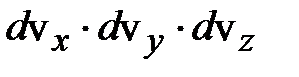 (рис.6.8,б). Таким образом,

.

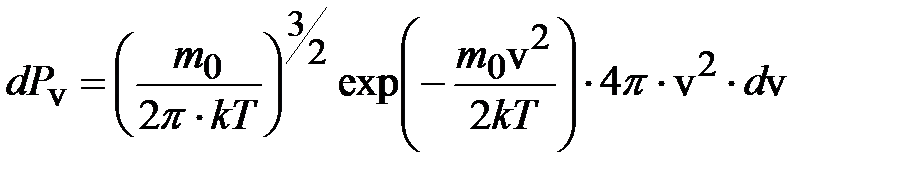Сравним полученное выражение с (6.48): 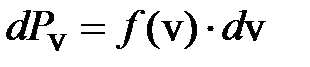, найдём функцию распределения по скоростям :

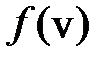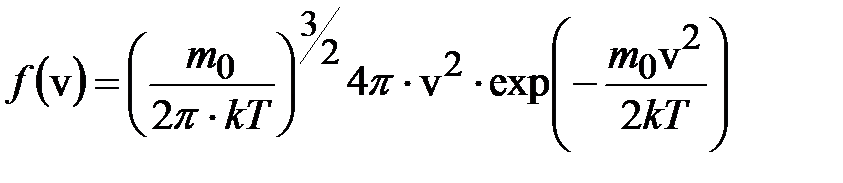 .                 (6.44)

а

б

Рис.6.9

T 2> T 1

T 1

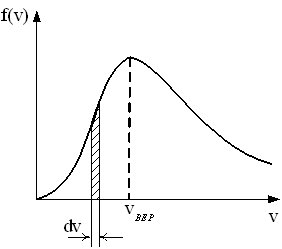
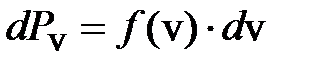На рис.6.9 представлен график функции. Значение функции f (v)=0 при v=0; при v→∞ функция также стремится к нулю. Функция достигает максимума при некоторой скорости, которую называют наиболее вероятной v_вер.. Заштрихованная полоска на рис.6.9,а равна вероятности  того, что скорость лежит в интервале 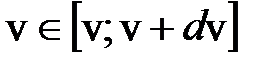. Вблизи наиболее вероятной скорости на единичный интервал скоростей приходится наибольшее число молекул. Вероятность того, что скорость лежит в конечном интервале от v₁ до v₂, равна интегралу:

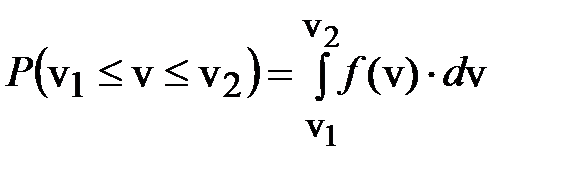.                                  (6.45)

По условию нормировки

,

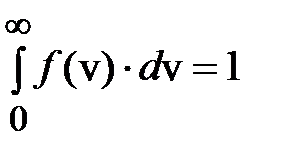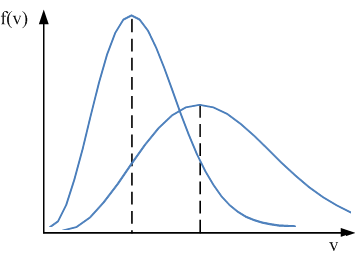
то есть площадь под всем графиком равна 1 и не изменится при изменении температуры. С ростом температуры (рис.6.9,б) скорости растут, v_вер. также становится больше, максимум смещается вправо, но максимальное значение функции уменьшается: график «расплывается», так как площадь под ним должна остаться равной 1.

 

7г. Характерные скорости: