3.1. Интегрирование систем линейных дифференциальных уравнений с
постоянными коэффициентами сведением к одному
дифференциальному уравнению
Многие системы дифференциальных уравнений, как однородные, так и неоднородные, могут быть сведены к одному уравнению относительно одной неизвестной функции. Покажем метод на примерах.
Пример 3.1. Решить систему 
Решение. 1) Дифференцируя по t первое уравнение и используя второе и третье уравнения для замены  и
и  , находим
, находим
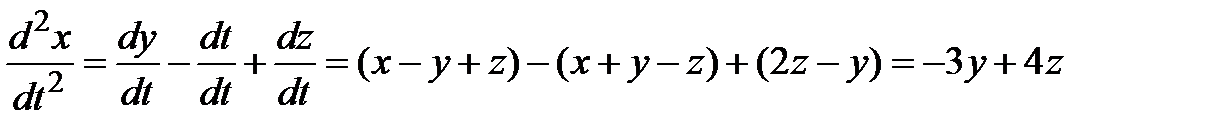 .
.
Полученное уравнение дифференцируем по  еще раз
еще раз
 .
.
1) Составляем систему

Из первых двух уравнений системы выразим переменные  и
и  через
через 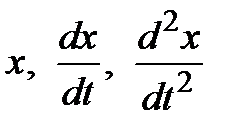 :
:
 . (3.1)
. (3.1)
Подставим найденные выражения для 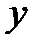 и
и  в третье уравнение системы
в третье уравнение системы
 .
.
Итак, для нахождения функции  получили дифференциальное уравнение третьего порядка с постоянными коэффициентами
получили дифференциальное уравнение третьего порядка с постоянными коэффициентами
 .
.
2) Интегрируем последнее уравнение стандартным методом: составляем характеристическое уравнение  , находим его корни
, находим его корни  и строим общее решение в виде линейной комбинации экспонент, учитывая кратность одного из корней:
и строим общее решение в виде линейной комбинации экспонент, учитывая кратность одного из корней:  .
.
3) Далее, чтобы найти две оставшиеся функции  и
и 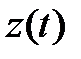 , дифференцируем дважды полученную функцию
, дифференцируем дважды полученную функцию 
 .
.
Используя связи (3.1) между функциями системы, восстанавливаем оставшиеся неизвестные

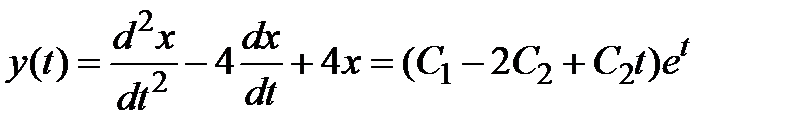 .
.
Ответ.  ,
,  ,
,  .
.
Может оказаться, что все известные функции кроме одной исключаются из системы третьего порядка уже при однократном дифференцировании. В таком случае, порядок дифференциального уравнения для ее нахождения будет меньше, чем число неизвестных функций в исходной системе.
Пример 3.2. Проинтегрировать систему
 (3.2)
(3.2)
Решение. 1) Дифференцируя по  первое уравнение, находим
первое уравнение, находим
 .
.
Исключая переменные  и
и  из уравнений
из уравнений

будем иметь уравнение второго порядка относительно 
 (3.3)
(3.3)
2) Из первого уравнения системы (3.2) имеем
 (3.4)
(3.4)
Подставляя в третье уравнение системы (3.2) найденные выражения (3.3) и (3.4) для 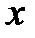 и
и  , получим дифференциальное уравнение первого порядка для определения функции
, получим дифференциальное уравнение первого порядка для определения функции 
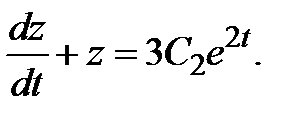
Интегрируя это неоднородное уравнение с постоянными коэффициентами первого порядка, найдем 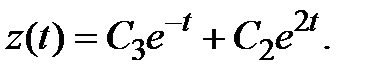 Используя (3.4), находим функцию
Используя (3.4), находим функцию 

Ответ.  ,
,  ,
, 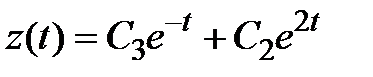 .
.
 2018-02-14
2018-02-14 566
566







