3.1.1.  3.1.2.
3.1.2. 
3.1.3.  3.1.4.
3.1.4. 
3.1.5.  3.1.6.
3.1.6. 
3.1.7.  3.1.8.
3.1.8. 
3.1.9.  3.1.10.
3.1.10. 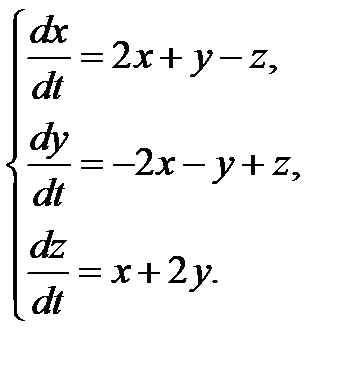
3.1.11.  3.1.12.
3.1.12. 
3.1.13.  3.1.14.
3.1.14. 
3.1.15.  3.1.16.
3.1.16. 
3.1.17.  3.1.18.
3.1.18. 
3.1.19.  3.1.20.
3.1.20. 
3.1.21. 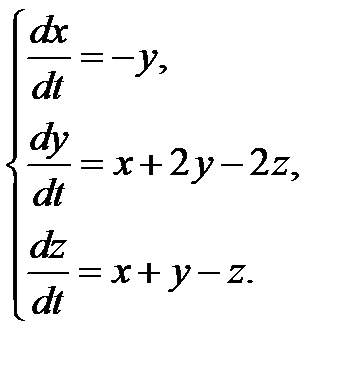 3.1.22.
3.1.22. 
3.1.23.  3.1.24.
3.1.24. 
3.1.25. 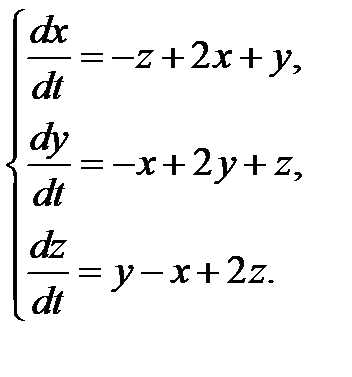 3.1.26.
3.1.26. 
3.1.27.  3.1.28.
3.1.28. 
3.1.29.  3.1.30.
3.1.30. 
3.2. Решение систем линейных однородных дифференциальных уравнений с постоянными коэффициентами с помощью нахождения
фундаментальной системы решений
Общее решение системы линейных однородных дифференциальных уравнений может быть найдено как линейная комбинация фундаментальных решений системы. В случае систем с постоянными коэффициентами для нахождения фундаментальных решений могут быть использованы методы линейной алгебры.
Пример 3.3. Решить систему
 (3.5)
(3.5)
Решение. 1) Перепишем систему в матричном виде
 . (3.6)
. (3.6)
2) Будем искать фундаментальное решение системы в виде вектора 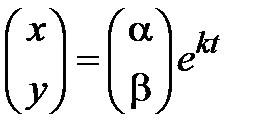 . Подставляя функции
. Подставляя функции  в (3.6) и сокращая на
в (3.6) и сокращая на  , получим
, получим

или
 , (3.7)
, (3.7)
то есть число  должно быть собственным числом матрицы
должно быть собственным числом матрицы 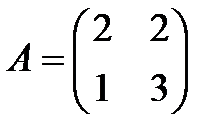 , а вектор
, а вектор 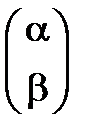 соответствующим собственным вектором.
соответствующим собственным вектором.
3) Из курса линейной алгебры известно, что система (3.7) имеет нетривиальное решение, если ее определитель равен нулю
 ,
,
то есть  . Отсюда находим собственные значения
. Отсюда находим собственные значения  .
.
4) Найдем соответствующие собственные векторы. Подставляя в (3.7) первое значение  , получим систему для нахождения первого собственного вектора
, получим систему для нахождения первого собственного вектора

или

Отсюда получаем связь между неизвестными  . Нам достаточно выбрать одно нетривиальное решение. Полагая
. Нам достаточно выбрать одно нетривиальное решение. Полагая  , тогда
, тогда  , то есть вектор
, то есть вектор  является собственным для собственного значения
является собственным для собственного значения 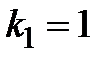 , а вектор функции
, а вектор функции  фундаментальным решением заданной системы дифференциальных уравнений (3.5). Аналогично, при подстановке второго корня
фундаментальным решением заданной системы дифференциальных уравнений (3.5). Аналогично, при подстановке второго корня  в (3.7) имеем матричное уравнение для второго собственного вектора
в (3.7) имеем матричное уравнение для второго собственного вектора  . Откуда получаем связь между его компонентами
. Откуда получаем связь между его компонентами  . Таким образом, имеем второе фундаментальное решение
. Таким образом, имеем второе фундаментальное решение
 .
.
5) Общее решение системы (3.5) строится как линейная комбинация двух полученных фундаментальных решений
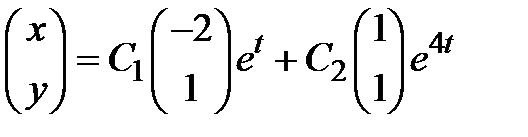
или в координатном виде
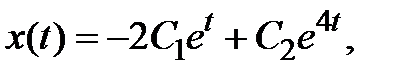
 .
.
Ответ. 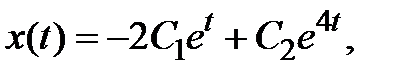
 .
.
 2018-02-14
2018-02-14 758
758








