2018-02-14
617
На основе регрессионного анализа можно определить отдельное влияние факторных признаков на результативный признак, для чего могут быть использованы дельта-коэффициенты и коэффициенты эластичности.
Дельта-коэффициент. Дельта-коэффициент определяетдолю вклада каждого фактора в суммарное влияние на выход:
, 
.
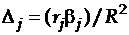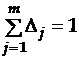При корректно проводимом регрессионном анализе все величины дельта-коэффициентов положительны, т.е. все коэффициенты регрессии имеют тот же знак, что и соответствующие коэффициенты парной корреляции. Только в случае мультиколлинеарности дельта-коэффициенты могут быть отрицательны [20,34,42].
Коэффициент эластичности. Влияние факторных признаков на результативный часто определяют также с использованием коэффициента эластичности. Эластичность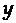 
по отношению к 
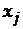определяется как процентное изменение 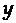, отнесенное к соответствующему процентному изменению 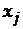. В общем случае эластичности не постоянны, они различаются, если измерены для различных точек на линии регрессии. По умолчанию стандартные программы, оценивающие эластичность, вычисляют ее в точках средних значений:
.
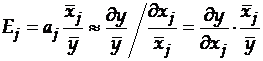Так, для линейной модели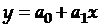 
коэффициент эластичности определяется по формуле: 
;
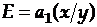для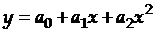 
: 
;
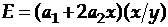для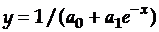 
: 
.
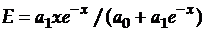Эластичность ненормирована и может изменяться в диапазоне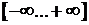 
. Важно, что она безразмерна, так что интерпретация эластичности 
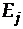=2.0 означает, что если 
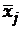увеличится (уменьшится) на 1%, то это приведет к увеличению (уменьшению) 
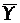на 2%. Если 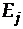= -0.5, то это означает, что увеличение 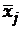на 1% приведет к уменьшению 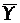на 0.5%.
Высокий уровень эластичности означает сильное влияние независимой переменной на объясняемую переменную. Для прогнозирования целесообразно рассчитывать эластичность на самых последних интервалах динамики [20,22,34,42].
