2018-02-14
1812
Временные экономические ряды могут иметь тенденции линейного или параметрического роста. При прогнозировании в этих случаях метод экспоненциального сглаживания выдает смещенные прогнозы. Для случая, когда временной ряд имеет тенденцию линейного роста, разработано несколько вариантов адаптивных моделей, также использующих процедуру экспоненциального сглаживания. В основе моделей лежит гипотеза о том, что прогноз может быть получен по уравнению
,
где 
- текущие оценки коэффициентов адаптивного полинома первого порядка.
Одной из первых моделей этого типа была двухпараметрическая модель Ч.Хольта, в которой оценка коэффициентов производится следующим образом:
;
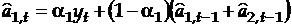где 
и 
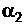- параметры экспоненциального сглаживания 
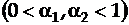, которые мы также будем называть параметрами адаптации.
Эти уравнения могут быть переписаны в виде:
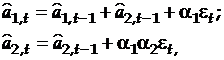
где 
- ошибка прогноза.
Частным случаем модели Хольта является модель линейного роста Брауна:
где параметр 
- коэффициент дисконтирования, характеризующий обесценение данных наблюдения за единицу времени, 0< <1.
Если модель Хольта усовершенствовать путем включения разности ошибок, то получим полную трехпараметрическую модель прогнозирования Дж. Бокса и Г. Дженкинса:
где 
, являются параметрами модели, 0< <1; - ошибка прогнозирования.
На основе практических испытаний модели на многих экономических рядах Бокс и Дженкинс пришли к выводу, что включение в модель разности ошибок не является необходимым. Коэффициент 
, всегда оказывался близким к нулю. П. Харрисон пришел к такому же заключению. Это объясняется стохастическим характером данных, и, в частности, тем, что корреляция ошибок в подобных случаях неустойчива.
Харрисон провел эмпирическое сравнение однопараметрической модели Брауна с многопараметрическими моделями. Многопараметрические модели ни в одном случае не дали заметного преимущества. Поэтому на практике для прогнозирования рядов с линейной тенденцией предпочтительнее использовать более простую модель Брауна. Из теоретического сопоставления различных моделей, проведенного П. Харрисоном и Д. Вардом, следует аналогичный вывод. К положительным чертам метода Брауна можно отнести следующие: логичная, ясная и легко понимаемая концепция; оптимальное значение единственного параметра можно быстро найти эмпирическим путем; коэффициенты модели прогнозирования оцениваются совместно таким образом, чтобы уменьшить автокорреляцию в остатках. Все это делает модель Брауна легко применимой [16,42].
Сезонные модели
Модели мультипликативной сезонности имеют вид:
,
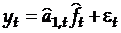где динамика величины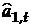 
характеризует тенденцию развития процесса;
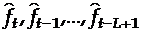- коэффициенты сезонности;
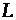- количество фаз в полном сезонном цикле (если ряд представляет месячные наблюдения, то в экономике обычно 
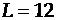, при квартальных данных 
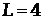и т. п.);
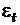- неавтокоррелированный шум с нулевым математическим ожиданием. Модели аддитивного типа записываются как:
,
где величина 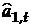описывает тенденцию развития процесса;
- аддитивные коэффициенты сезонности.
Адаптивная модель линейного роста с мультипликативной сезонностью была предложена П. Р. Уинтерсом. Аддитивная модель рассмотрена Г. Тейлом и С. Вейджем.
Модель с мультипликативной сезонностью имеет вид:
Как видим, 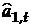является взвешенной суммой текущей оценки 
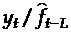, полученной путем очищения от сезонных колебаний фактических данных 
и предыдущей оценки 
. В качестве коэффициента сезонности 
берется его наиболее поздняя оценка, сделанная для аналогичной фазы цикла. Затем величина 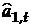, полученная по первому уравнению, используется для определения новой оценки коэффициента сезонности по второму уравнению.
Прогноз следующего значения ряда:
.
Общее выражение прогноза на 
шагов вперед:
.
Величины 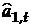и могут быть записаны через прошлые данные и начальные условия:
,
где 
- начальное значение 
; 
- начальное значение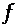 
в соответствующей 
фазе цикла; - наибольшая целая часть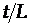 
.
Следовательно, прогноз является функцией всех прошлых значений ряда, параметров и 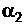, и начальных условий 
Модель аддитивной сезонности строится аналогично с той лишь разницей, что уровень ряда определяется соотношением:
.
Влияние начальных условий на прогноз зависит от величины весов и длины ряда, предшествующего текущему моменту 
. Влияние обычно будет уменьшаться быстрее, чем влияние начальных значений , так как 
, пересматривается на каждом шаге, а 
только один раз за цикл.
Если эта сезонная модель прогнозирования, структура которой не содержит элементов для отражения какой-либо тенденции роста, применяется для прогнозирования ряда, характеризующегося ярко выраженной тенденцией, то коэффициенты перестают быть простыми коэффициентами сезонности и вскоре вбирают в себя в определенной мере эффект роста.
