Простое экспоненциальное сглаживание

Экспоненциальное сглаживание - один из простейших и распространенных приемов выравнивания ряда. В его основе лежит расчет экспоненциальных средних.

Экспоненциальное сглаживание ряда 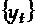 осуществляется по рекуррентной формуле

,

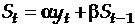где  - значение экспоненциальной средней в момент ;

 - параметр сглаживания,  = const, 0< <1; =1- .

 Это выражение можно переписать следующим образом:

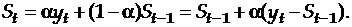
Экспоненциальная средняя на момент  здесь выражена как экспоненциальная средняя предшествующего момента плюс доля разницы текущего наблюдения и экспоненциальной средней прошлого момента.

Величина  является взвешенной суммой всех членов ряда. Причем веса падают экспоненциально в зависимости от давности («возраста») наблюдения. Это и объясняет, почему величина , названа экспоненциальной средней [16].

Экспоненциальная средняя , имеет тоже математическое ожидание, что и временной ряд, но меньшую дисперсию:

.               

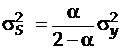При высоком значении  дисперсия экспоненциальной средней незначительно отличается от дисперсии ряда. Чем меньше , тем в большей степени сокращается дисперсия экспоненциальной средней. Следовательно, экспоненциальное сглаживание можно представить как фильтр, на вход которого в виде потока последовательно поступают члены исходного ряда, а на выходе формируются текущие значения экспоненциальной средней. И чем меньше , тем в большей степени фильтруются, подавляются колебания исходного ряда.

Рассмотрим ряд, генерированный моделью

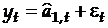
где 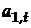 - варьирующий во времени средний уровень ряда;  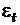- случайные неавтокоррелированные отклонения, или шум, со средним значением 0 и дисперсией .

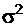Прогнозная модель имеет вид:

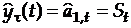
Прогноз, сделанный в момент  на  шагов вперед оценивается по экспоненциальной средней. Новый прогноз получается в результате корректировки предыдущего прогноза с учетом его ошибки .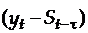

При краткосрочном прогнозировании желательно как можно быстрее отразить изменения 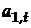 и в то же время как можно лучше «очистить» ряд от случайных колебаний.

Таким образом, с одной стороны, следует увеличивать вес более свежих наблюдений, что может быть достигнуто повышением 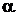, с другой стороны, для сглаживания случайных отклонений величину  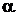нужно уменьшить. Как видим, эти два требования находятся в противоречии. Поиск компромиссного значения и составляет задачу оптимизации модели.