Обчислення похибки відліку (округлення)

При фізичних вимірюваннях відлік показання приладів часто округлюються. В результаті виникають похибки округлення. Інтервал округлення може бути різним. Якщо відлік проводиться з точністю до цілої поділки, то інтервал округлення дорівнює ціні найменшої поділки шкали приладу; якщо відлік округлюється до половини поділки, інтервал округлення дорівнює половині ціни поділки і т.д. Максимальна похибка округлення, очевидно, не повинна перевищувати половини інтервалу округлення, т.б. величини h. Тоді для довірної ймовірності р= 0,95 абсолютна похибка відліку обчислюється за формулою:

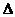х _окр = р

Приклад: довжину деякого предмета вимірюють за допомогою масштабної лінійки з міліметровими поділками. Відлік проводиться з точністю до 1мм.Тоді,

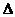х _окр = р  = 0,95  = 0,48 мм 0,5 мм

Обчислення повної похибки прямого вимірювання.

У теорії ймовірностей встановлено що похибка, зумовлена декількома незалежними причинами, визначається “квадратичним” додаванням всіх складових повної похибки..

Як відомо, в навчальних лабораторіях, крім поправок, що вводяться в результат безпосередньо, враховуються три складові похибки прямих вимірювань: випадкова похибка 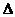х _вип, похибка приладу 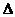х _пр і похибка відліку (округлення) 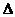х _окр. Повна абсолютна похибка прямого вимірювання визначається за формулою:

Відносна похибка прямого вимірювання обчислюється за формулою:

При розрахунках всіх складових похибок довірна ймовірність приймається однаковою р =0,95. Якщо одна із складових похибок в три рази менша іншої, то її внесок в загальну суму похибок незначний і такою похибкою можна знехтувати.

Оцінка похибок непрямих вимірювань.